
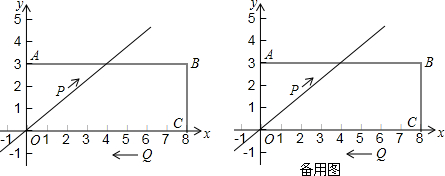
分析 (1)由直线y=$\frac{3}{4}$x交AB于点D,矩形OABC的顶点A坐标为(0,3),把y=4代入y=$\frac{3}{4}$x得,解得x=4,即可求出点D的坐标
(2)分两种情况①当PC=PB时,②当PB=BC时,设P(x,$\frac{3}{4}$x)分别求解即可,
(3)分两种情况:①当PQ⊥x轴,由PQ=$\frac{3}{5}$at,PQ=$\frac{3}{4}$(8-t),可得a的值,由△OPQ∽△BCQ,得出$\frac{PQ}{BC}$=$\frac{OQ}{CQ}$,解得t的值,即可得出a的值,或利用$\frac{PQ}{CQ}$=$\frac{OQ}{BC}$t的值,即可解得a的值,②当PQ⊥OD,由PQ=$\frac{3}{4}$at,PQ=$\frac{3}{5}$(8-t),可得a的值,由△OPQ∽△BCQ,可得$\frac{PQ}{BC}$=$\frac{OP}{CQ}$,解得t的值,即可得出a的值,$\frac{PQ}{CQ}$=$\frac{OP}{BC}$,解得t的值,代入求得a的值.
解答 解:(1)∵直线y=$\frac{3}{4}$x交AB于点D,矩形OABC的顶点A坐标为(0,3),
∴把y=4代入y=$\frac{3}{4}$x得,3=$\frac{3}{4}$x,解得x=4,
∴D(4,3);
(2)①如图1,当PC=PB时,点P为BC的中垂线与直线y=$\frac{3}{4}$x的交点,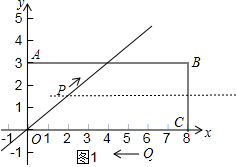
∴把y=$\frac{3}{2}$代入y=$\frac{3}{4}$x得,$\frac{3}{2}$=$\frac{3}{4}$x,解得x=2,
∴${P_1}({2,\frac{3}{2}})$;
②如图2,当PB=BC时,设P(x,$\frac{3}{4}$x)
∵B(8,3),
∴PB2=(x-8)2+($\frac{3}{4}$x-3)2,
∴(x-8)2+($\frac{3}{4}$x-3)2=9,解得x1=$\frac{128}{25}$,x2=8(舍去)
∴把x1=$\frac{128}{25}$代入y=$\frac{3}{4}$x,得y=$\frac{96}{25}$,
∴${P_2}({\frac{128}{25},\frac{96}{25}})$;
(3)①如图3,当PQ⊥x轴,连接BQ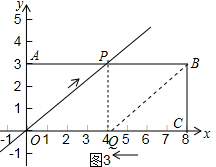
PQ=$\frac{3}{5}$at,PQ=$\frac{3}{4}$(8-t),
∴a=$\frac{40-5t}{4t}$,
∵△OPQ∽△BCQ,
∴$\frac{PQ}{BC}$=$\frac{OQ}{CQ}$,即$\frac{\frac{3}{4}(8-t)}{3}$=$\frac{8-t}{t}$,解得t=4
a=$\frac{40-5t}{4t}$=$\frac{5}{4}$,
或$\frac{PQ}{CQ}$=$\frac{OQ}{BC}$即$\frac{\frac{3}{4}(8-t)}{t}$=$\frac{8-t}{3}$,解得t=$\frac{9}{4}$,
把t=$\frac{9}{4}$代入a=$\frac{40-5t}{4t}$,解得a=$\frac{115}{36}$,
∴∠OQP=90°时,$a=\frac{5}{4}或\frac{115}{36}$;
②如图4,当PQ⊥OD,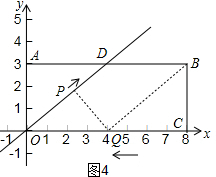
∵PQ=$\frac{3}{4}$at,PQ=$\frac{3}{5}$(8-t),
∴a=$\frac{32-4t}{5t}$,
∵△OPQ∽△BCQ,
∴$\frac{PQ}{BC}$=$\frac{OP}{CQ}$,即$\frac{\frac{3}{4}at}{3}$=$\frac{at}{8-t}$,解得t=4,
把t=4代入a=$\frac{32-4t}{5t}$=$\frac{4}{5}$,
或$\frac{PQ}{CQ}$=$\frac{OP}{BC}$,即$\frac{\frac{3}{4}at}{t}$=$\frac{at}{3}$,解得t=$\frac{9}{4}$,
把t=$\frac{9}{4}$,代入a=$\frac{32-4t}{5t}$=$\frac{92}{45}$,
∴∠OPQ=90°时,$a=\frac{4}{5}或\frac{92}{45}$.
点评 本题主要考查了一次函数综合题,涉及一次函数中求点的坐标,等腰三角形的性质及相似三角形的性质,解题的关键是分不同情况解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图所示是长方形养鸡场平面示意图,一面靠墙,且墙长为18米,另外三面用竹篱笆围成,若竹篱笆总长为35m,围的面积为150m2,则此长方形鸡场的长、宽分别为15米、10米.
如图所示是长方形养鸡场平面示意图,一面靠墙,且墙长为18米,另外三面用竹篱笆围成,若竹篱笆总长为35m,围的面积为150m2,则此长方形鸡场的长、宽分别为15米、10米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
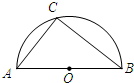 如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 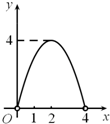 | B. | 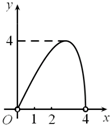 | C. | 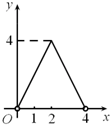 | D. | 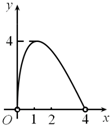 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
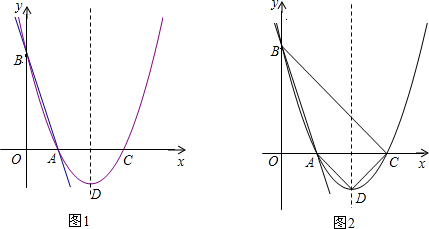
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
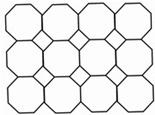 如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要12个小正方形,14小三角形.(不含图案的4个角)
如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要12个小正方形,14小三角形.(不含图案的4个角)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
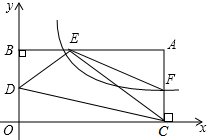 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
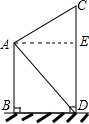 如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
如图,甲楼的底端B处与乙楼的底端D处相距50m,从甲楼顶部A处看乙楼顶部C处的仰角∠CAE的度数为20°.从甲楼顶部A处看乙楼底部D处的俯角∠DAE的度数为35.分别求甲楼AB和乙楼CD的高为多少m(精确到1m).(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -212 | B. | -$\frac{1}{10}$ | C. | -0.01 | D. | -5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com