
分析 假设三角形的三个内角∠A、∠B、∠C中有两个直角,∠A+∠B+∠C>180°,假设三角形的三个内角∠A、∠B、∠C中有两个钝角∠A+∠B+∠C>180°,这都与三角形内角和为180°相矛盾,因此三角形中不能有两个角是直角或钝角.
解答 证明:
假设三角形的三个内角∠A、∠B、∠C中有两个直角,不妨设∠A=∠B=90°,
则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,
∴∠A=∠B=90°不成立;
所以一个三角形中不能有两个直角.
假设三角形的三个内角∠A、∠B、∠C中有两个钝角,不妨设∠A和∠B为钝角,
则∠A+∠B+∠C>180°,这与三角形内角和为180°相矛盾,
∴∠A和∠B为钝角不成立;
所以一个三角形中不能有两个钝角.
综上:三角形中不能有两个角是直角或钝角.
点评 此题主要考查了反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:
(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
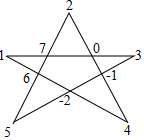 如图所示,将数字-2,-1,0,1,2,3,4,5,6,7这10个数字分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的四个数相加,共得5个数.设为a1,a2,a3,a4,a5,求$\frac{1}{2}$(a1+a2+a3+a4+a5)的值;变换其中任何两数的位置后,$\frac{1}{2}$(a1+a2+a3+a4+a5)的值是否改变?说明理由.
如图所示,将数字-2,-1,0,1,2,3,4,5,6,7这10个数字分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的四个数相加,共得5个数.设为a1,a2,a3,a4,a5,求$\frac{1}{2}$(a1+a2+a3+a4+a5)的值;变换其中任何两数的位置后,$\frac{1}{2}$(a1+a2+a3+a4+a5)的值是否改变?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
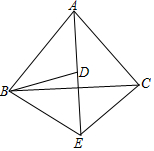 如图所示,已知$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$.∠ABD=20°,求∠EBC的大小.
如图所示,已知$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$.∠ABD=20°,求∠EBC的大小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+4=0}\\{\frac{1}{x}-5>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{x}^{2}-x=0}\\{x+1<0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+2>0}\\{x-y<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x-5>0}\\{x<0}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com