
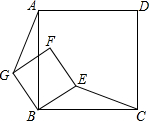
 如图,正方形ABCD和正方形GBEF,连接AG、CE,猜想CE与AG的位置关系,并证明你的猜想.
如图,正方形ABCD和正方形GBEF,连接AG、CE,猜想CE与AG的位置关系,并证明你的猜想. 分析 连接AC,延长CE交AG于M,由正方形的性质得出AB=BC,BG=BE,∠ABC=∠GBE=90°,∠BAC=∠BCA=45°,证出∠ABG=∠CBE,由SAS证明ABG≌△CBE,得出∠BAG=∠BCE,证出∠ECA+∠MAC=90°,即可得出结论.
解答 解:CE⊥AG;理由如下:
连接AC,延长CE交AG于M,如图所示:
∵四边形ABCD和四边形GBEF是正方形,
∴AB=BC,BG=BE,∠ABC=∠GBE=90°,∠BAC=∠BCA=45°,
∴∠ABG=∠CBE,
在△ABG和△CBE中,
$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABG=∠CBE}&{\;}\\{BG=BE}&{\;}\end{array}\right.$,
∴ABG≌△CBE(SAS),
∴∠BAG=∠BCE,
∴∠ECA+∠MAC=∠ECA+∠BAG+∠BAC=∠ECA+∠BCE+45°=45°+45°=90°,
∴∠AMC=90°,
∴CE⊥AG.
点评 本题考查了正方形的性质、全等三角形的判定与性质、垂线的证明方法;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).
如图,某校在开展积极培育和践行社会主义核心价值观的活动中,小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上,制成卡片,随时提醒自己要做个遵纪守法的好学生.小光同学还把卡片编成一道数学题考同桌小亮:将这4张卡片洗匀后背面朝上放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取另一张卡片,让小亮同学用列表法或画树状图法,求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率(卡片名称可用字母表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
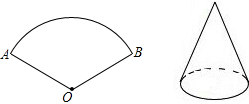 如图,将面积为108πcm2,半径为18cm的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是12$\sqrt{2}$cm.
如图,将面积为108πcm2,半径为18cm的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是12$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com