
【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
【答案】(1)6;(2) 930人;(3) 经典诗词诵背系列活动效果好,理由见解析
【解析】
(1)根据中位数的定义进行解答,即中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);
(2)用总人数乘以大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数所占的百分比即可;
(3)根据活动初的平均数、中位数与活动后的平均数、中位数进行比较,即可得出答案.
(1)∵把这些数从小到大排列,最中间的数是第20和21个数的平均数,则中位数是![]() (首);
(首);
(2)根据题意得:
![]() (人),
(人),
估计大赛后一个月该校学生一周诗词背6首(含6首)以上的人数为930人.
(3)①活动初40名学生平均背诵首数为![]() (首),
(首),
活动1个月后40名学生平均背诵首数为![]() (首);
(首);
②活动初学生一周诗词诵背数量中位数为6,活动一个月后学生一周诗词诵背数量中位数为7;
根据以上数据分析,该校经典诗词诵背系列活动效果好.


科目:初中数学 来源: 题型:
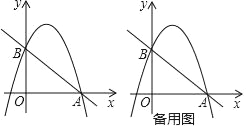
【题目】已知:如图,抛物线y=﹣x2+bx+C经过点B(0,3)和点A(3,0)
(1)求该抛物线的函数表达式和直线AB的函数表达式;
(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
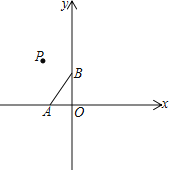
【题目】已知:平面直角坐标系中,点A(-2,0)、B(0,3),点P为第二象限内一点
(1) 如图,将线段AB绕点P旋转180°得线段CD,点A与点C对应,试画出图形;
(2) 若(1)中得到的点C、D恰好在同一个反比例函数![]() 的图象上,试求直线BC的解析式;
的图象上,试求直线BC的解析式;
(3) 若点Q(m,n)为第四象限的一点,将线段AB绕点Q顺时针旋转90°到点E、F.若点E、F恰好在同一个反比例函数的图象上,试直接写出m、n之间的关系式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.
(1)求购买一个甲奖品和一个乙奖品各需多少元?
(2)经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图![]() 是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数
是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数![]() ,
, ![]() ,
, ![]() ,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为
,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为![]() (如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图
(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图![]() 是背面完全一样、牌面数字分别是
是背面完全一样、牌面数字分别是![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为
的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌的牌面数字记为![]() .计算
.计算![]() 的值.
的值.


(![]() )用树状图或列表法求
)用树状图或列表法求![]() 的概率.
的概率.
(![]() )甲乙两人玩游戏,规定:当
)甲乙两人玩游戏,规定:当![]() 是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由.
是正数时,甲胜;否则,乙胜,你认为这个游戏规则对甲乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校决定从甲、乙两名同学中选拔一人参加“诵读经典”大赛,在相同的测试条件下,甲、乙两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83.
乙:88,81,85,81,80.
请回答下列问题:
(1)甲成绩的中位数是______,乙成绩的众数是______;
(2)经计算知![]() ,
,![]() .请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
.请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
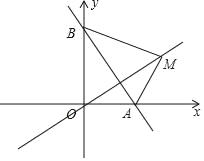
【题目】如图,在平面直角坐标系中,A(p,0),B(0,q),且p、q满足(p﹣2)2+![]() =0.
=0.
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是以AB为底的等腰直角三角形,求m值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com