
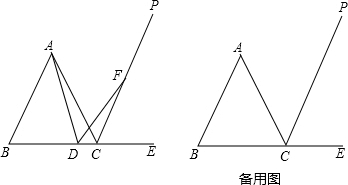
分析 (1)①先由等边三角形得:各内角为60°,再根据外角定理在△ABD中得:∠ADE=∠B+∠BAD,并由∠ADE在图形中分成的两角和得出∠BAD=∠CDF;
②利用外角平分线得:∠ACP=∠PCE=60°,证明A、D、C、F四点共圆,从而得出△ADF是等边三角形,所以AD=FD;
(2)第一个结论不一定正确,第二个结论一定正确,理由是:如图2,同理连接AF,根据角的和差得:∠BAD=60°+∠CAD,∠CDF=60°+∠ADC,而且而D是射线BC上任意一点;CD与AC不一定相等,只有相等时两角才相等;第二个结论与②同理得:A、C、D、F四点共圆,则△ADF 是等边三角形,所以AD=FD.
解答 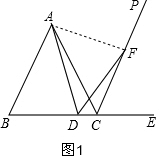 证明:(1)如图1,①∵△ABC是等边三角形,
证明:(1)如图1,①∵△ABC是等边三角形,
∴∠B=∠ACB=∠BAC=60°,
∵∠ADE=∠B+∠BAD,∠ADE=∠CDF+∠ADF,
∴∠B+∠BAD=∠CDF+∠ADF,
∵∠ADF=60°,
∴∠B=∠ADF,
∴∠BAD=∠CDF;
②连接AF,
∵∠ACB=60°,
∴∠ACE=120°,
∵CP平分∠ACE,
∴∠ACP=∠PCE=60°,
∴∠ADF=∠ACP=60°,
∴A、D、C、F四点共圆,
∴∠AFD=∠ACB=60°,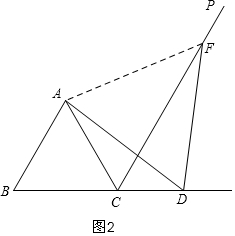
∴∠ADF=∠AFD=60°,
∴∠DAF=60°,
∴△ADF是等边三角形,
∴AD=FD;
(2)若点D在线段BC的延长线上,(1)中的第一个结论不一定正确,第二个结论一定正确,理由是:
如图2,连接AF,
∵∠BAD=∠BAC+∠CAD,∠BAC=60°,
∴∠BAD=60°+∠CAD,
∵∠CDF=∠ADC+∠ADF,∠ADF=60°,
∴∠CDF=60°+∠ADC,
只有当∠CAD=∠ADC时,第一个结论正确,即∠BAD=∠CDF,而只有CD=AC时两角才相等;而D是射线BC上任意一点;
同(1)得:∠ADF=∠ACF=60°,
∴A、C、D、F四点共圆,
∴∠FAD=∠FCD=60°,
∴∠AFD=60°,
∴△ADF 是等边三角形,
∴AD=FD.
点评 本题考查了等边三角形的性质和判定及三角形的外角定理,知道等边三角形的三边相等,且各角为60°;本题多次运用了外角定理和角的和差关系得出角的大小关系;同时本题利用了四点共圆,若线段同侧二点到线段两端点连线夹角相等,则四点共圆;本题也可以过D作DG∥AC,得出结论.


科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(-3,0),C(0,-3)
如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(-3,0),C(0,-3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 股票名称 | 每股净赚(元) | 股数 |
| 长城 | +23 | 500 |
| 北斗 | -3 | 1000 |
| 白马 | +1.5 | 1000 |
| 海潮 | -7 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)×(-$\frac{3}{2}$)×$\frac{2}{3}$ | B. | (-1)×(-$\frac{3}{2}$)×$\frac{3}{2}$ | C. | (-1)×(-$\frac{2}{3}$)×$\frac{3}{2}$ | D. | (-1)×(-$\frac{2}{3}$)×$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
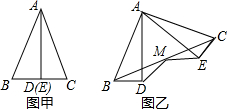 已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.
已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.
如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com