
【题目】抛物线![]() 与
与![]() 轴交于点C(0,3),其对称轴与
轴交于点C(0,3),其对称轴与![]() 轴交于点A(2,0).
轴交于点A(2,0).
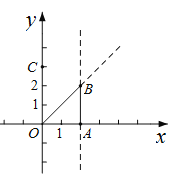
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 适当平移,使平移后的抛物线
适当平移,使平移后的抛物线![]() 的顶点为D(0,
的顶点为D(0,![]() ).已知点B(2,2),若抛物线
).已知点B(2,2),若抛物线![]() 与△OAB的边界总有两个公共点,请结合函数图象,求
与△OAB的边界总有两个公共点,请结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由抛物线![]() 与
与![]() 轴交于点C(0,3),得到
轴交于点C(0,3),得到![]() ;由抛物线
;由抛物线![]() 的对称轴为
的对称轴为![]() ,得到
,得到![]() 的值,从而得到抛物线
的值,从而得到抛物线![]() 的解析式;
的解析式;
(2)设抛物线![]() 的解析式为
的解析式为![]() ,当抛物线经过点A(2,0)时,解得
,当抛物线经过点A(2,0)时,解得![]() ,由O(0,0),B(2,2),得到直线OB的解析式为
,由O(0,0),B(2,2),得到直线OB的解析式为![]() .联立得方程
.联立得方程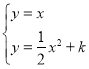 ,得
,得![]() ,当Δ=
,当Δ=![]() =0,即
=0,即![]() 时,抛物线
时,抛物线![]() 与直线OB只有一个公共点,此时方程化为
与直线OB只有一个公共点,此时方程化为![]() ,解得
,解得![]() ,即公共点P的横坐标为1,点P在线段OB上,即可得到
,即公共点P的横坐标为1,点P在线段OB上,即可得到![]() 的取值范围是
的取值范围是![]() .
.
解:(1)∵抛物线![]() 与
与![]() 轴交于点C(0,3),
轴交于点C(0,3),
∴![]() ;
;
∵抛物线![]() 的对称轴为
的对称轴为![]() ,
,
∴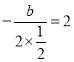 ,解得
,解得![]() ,
,
∴抛物线![]() 的解析式为
的解析式为![]() ;
;
(2)由题意,抛物线![]() 的解析式为
的解析式为![]() ,当抛物线经过点A(2,0)时,
,当抛物线经过点A(2,0)时,![]() ,解得
,解得![]() ,
,
∵O(0,0),B(2,2),
∴直线OB的解析式为![]() .由
.由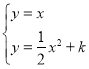 ,得
,得![]() ,
,
当Δ=![]() =0,即
=0,即![]() 时,抛物线
时,抛物线![]() 与直线OB只有一个公共点,此时方程化为
与直线OB只有一个公共点,此时方程化为![]() ,解得
,解得![]() ,即公共点P的横坐标为1,点P在线段OB上,
,即公共点P的横坐标为1,点P在线段OB上,
∴![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
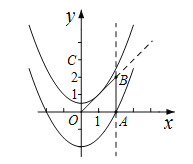
【题目】二次函数y=ax2+bx+c的图象如图,对称轴是直线x=﹣1,有以下结论:①abc>0;②4ac<b2;③2a﹣b=0;④a﹣b+c>0;⑤9a﹣3b+c>0.其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
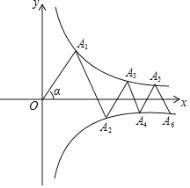
【题目】如图,点A1、A3、A5…在反比例函数y=![]() (x>0)的图象上,点A2、A4、A6……在反比例函数y=-
(x>0)的图象上,点A2、A4、A6……在反比例函数y=-![]() (x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
(x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
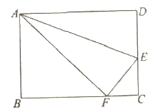
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕AE=10![]() ,且CE:CF=4:3,那么该矩形的周长为( )
,且CE:CF=4:3,那么该矩形的周长为( )
A.48B.64C.92D.96
查看答案和解析>>
科目:初中数学 来源: 题型:
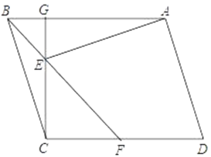
【题目】如图,在ABCD中,CG⊥AB于点G,∠ABF=45°,F在CD上,BF交CG于点E,连接AE,且AE⊥AD.
(1)若BG=2,BC=![]() ,求EF的长度;
,求EF的长度;
(2)求证:CE+![]() BE=AB.
BE=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,直线 l:![]() 与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线
与 x 轴交于点 A(-2,0),与 y 轴交于点 B.双曲线![]() 与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
与直线 l 交于 P,Q 两点,其中点 P 的纵坐标大于点 Q 的纵坐标.
(1)求点 B 的坐标;
(2)当点 P 的横坐标为 2 时,求 k 的值;
(3)连接 PO,记△POB 的面积为 S,若![]() ,直接写出 k 的取值范围.
,直接写出 k 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
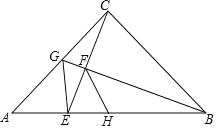
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10![]() ,则BF=4
,则BF=4![]() ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
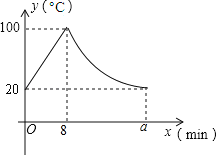
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)与通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温y(℃)与通电时间x(min)的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求y与x之间的函数关系式;
(2)求出图中a的值;
(3)某天早上7:20,李老师将放满水后的饮水机电源打开,若他想在8:00上课前能喝到不超过40℃的温开水,问:他应在什么时间段内接水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com