
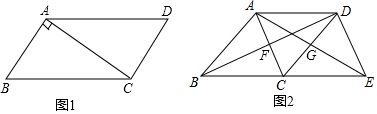
���� ��1�����ù��ɶ������AC�ij������ж���
��2������ͼ2�У��ɡ�4=��5+��CAE����2=��BDC+��6����5=��6��ֻҪ֤����2=��4���ɽ�����⣻
��������AB=CD=DE=EG����CD=DE=EG=4a����GH=DH=a��CH=3a�����AD���ɽ�����⣻
��� �⣺��1����ͼ1�У�ƽ���ı���ABCD�ǡ������ı��Ρ���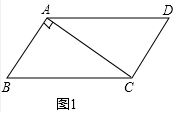
��Rt��ABC�У��ߡ�BAC=90�㣬AB=1��BC=$\sqrt{5}$��
��AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=2��
��AC=2AB��
��ƽ���ı���ABCDΪ�������ı��Ρ���
��2������ͼ2�У�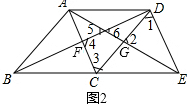
���ı���ABCD��ƽ���ı��Σ��ı���ACED��ƽ���ı��Σ�
��BF=DF��AG=GE��
��BD��AEΪ�������Խ��ߡ���CD��DEΪ�������ߡ���
��DC=DF��ED=EG��
���3=��4����1=��2��
��AC��DE��
���1=��3��
���2=��4��
�ߡ�4=��5+��CAE����2=��BDC+��6����5=��6��
���CAE=��BDC��
����ͼ3�У���EH��CD��H��
������AB=CD=DE=EG����CD=DE=EG=4a����GH=DH=a��CH=3a��
��Rt��DHE��EH=$\sqrt{E{G}^{2}-G{H}^{2}}$=$\sqrt{15}$a��
��Rt��CHE��CE=$\sqrt{C{H}^{2}+E{H}^{2}}$=$\sqrt{��3a��^{2}+��\sqrt{15}a��^{2}}$=2$\sqrt{6}$a��
��AD=CE=2$\sqrt{6}$a��
��$\frac{AD}{DE}$=$\frac{2\sqrt{6}a}{4a}$=$\frac{\sqrt{6}}{2}$��
���� ���⿼�����������ε����ʡ�ƽ���ı��ε����ʡ����ɶ��������������ε����ʡ������ε���ǵ����ʵ�֪ʶ������Ĺؼ����������⣬���������ѧ֪ʶ������⣬ѧ�����ò���������⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
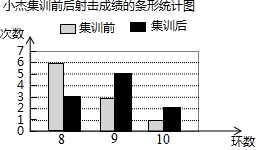 Ϊ�˽�����˶�ԱС�ܵļ�ѵЧ��������ͳ��������ѵǰ������β��Գɼ���ÿ�β������10�Σ�����������ͼ��ʾ������ͳ��ͼ��
Ϊ�˽�����˶�ԱС�ܵļ�ѵЧ��������ͳ��������ѵǰ������β��Գɼ���ÿ�β������10�Σ�����������ͼ��ʾ������ͳ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��1 | B�� | m��0 | C�� | m��1 | D�� | m��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
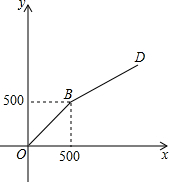 ����һ����ͯ���ڼ䣬�ס�������������ͬ���۸�������ͬ�Ķ�ͯ��Ʒ�����ǵ��Żݷ����ֱ�Ϊ���꣬һ���Թ��ﳬ��100Ԫ��ļ۸ִ����ۣ��ҵ꣬һ���Թ��ﳬ��500Ԫ��ļ۸ִ����ۣ�����Ʒԭ��ΪxԪ������Ӧ�����ΪyԪ��
����һ����ͯ���ڼ䣬�ס�������������ͬ���۸�������ͬ�Ķ�ͯ��Ʒ�����ǵ��Żݷ����ֱ�Ϊ���꣬һ���Թ��ﳬ��100Ԫ��ļ۸ִ����ۣ��ҵ꣬һ���Թ��ﳬ��500Ԫ��ļ۸ִ����ۣ�����Ʒԭ��ΪxԪ������Ӧ�����ΪyԪ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
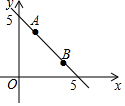 ��ͼ����֪һ�κ���y=mx+5��ͼ����A��1��4����B��n��2����
��ͼ����֪һ�κ���y=mx+5��ͼ����A��1��4����B��n��2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
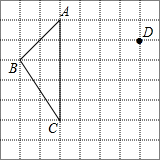 ��ͼ���ڷ���ֽ�У���֪����ABC������һ��D��ƽ�ơ�ABC��ʹ��A�ƶ�����D�����������ͼ��
��ͼ���ڷ���ֽ�У���֪����ABC������һ��D��ƽ�ơ�ABC��ʹ��A�ƶ�����D�����������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com