

 (2)过点Q作QP⊥AD,垂足即为点P(3)证明见解析
(2)过点Q作QP⊥AD,垂足即为点P(3)证明见解析 ;…………………………………………………………2分
;…………………………………………………………2分 =
= .…………………………6分
.…………………………6分 .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:不详 题型:解答题
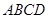 是矩形纸片,翻折∠
是矩形纸片,翻折∠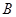 、∠
、∠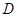 使
使 边、
边、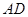 边恰好落在
边恰好落在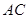 上。设
上。设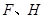 分别是
分别是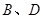 落在AC上的两点,
落在AC上的两点,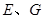 分别是折痕
分别是折痕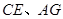 与
与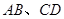 的交点。
的交点。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的
,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的 的度数是 (▲ )
的度数是 (▲ )
| A.110° | B.120° | C.140° | D.150° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com