
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 上的动点.
上的动点.

(1)能否在线段![]() 上作出点E,在线段
上作出点E,在线段![]() 上作出点
上作出点![]() ,使
,使![]() 的周长最小?______(用“能”或“不能”填空);
的周长最小?______(用“能”或“不能”填空);
(2)如果能,请你在图中作出满足条件的点![]() 、
、![]() (不要求写出作法),并直接写出
(不要求写出作法),并直接写出![]() 的度数;如果不能,请说明理由.
的度数;如果不能,请说明理由.
【答案】(1)能;(2)作出满足条件的点![]() 、
、![]() (图见解析),
(图见解析),![]()
【解析】
(1)根据对称性能在线段AD上作出点E,在线段DC上作出点F,使△BEF的周长最小;
(2)根据对称性得等腰三角形,再根据三角形内角和即可求出∠EBF的度数.
解:(1)能在线段AD上作出点E,在线段DC上作出点F,使△BEF的周长最小.
故答案为:能.
(2)如图所示: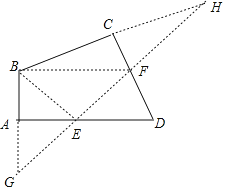
点E、F即为所求作的点.
作点B关于AD和DC的对称点G和H,
连接GH,交AD和DC于点E和F,
连接BE、BF,此时△BEF的周长最小.
由对称性可知:
BF=HF,BE=GE,
∴∠FBH=∠H,∠EBG=∠G,
∵四边形ABCD中,∠D=70°,∠A=∠C=90°,
∴∠ABC=110°,
∴∠H+∠G=70°,
∴∠FBH+∠EBG=70°,
∴∠EBF=110°-70°=40°.


科目:初中数学 来源: 题型:
【题目】对于△ABC及其边上的点P,给出如下定义:如果点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 都在△ABC的边上,且
都在△ABC的边上,且![]() ,那么称点
,那么称点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距点,线段
为△ABC关于点P的等距点,线段![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距线段.
为△ABC关于点P的等距线段.
(1)如图1,△ABC中,∠A<90°,AB=AC,点P是BC的中点.

①点B,C △ABC关于点P的等距点,线段PA,PB △ABC关于点P的等距线段;(填“是”或“不是”)
②△ABC关于点P的两个等距点![]() ,
,![]() 分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段
分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段![]() ,
,![]() ;
;
(2)△ABC是边长为4的等边三角形,点P在BC上,点C,D是△ABC关于点P的等距点,且PC=1,求线段DC的长;
(3)如图2,在Rt△ABC中,∠C=90°,∠B=30°.点P在BC上,△ABC关于点P的等距点恰好有四个,且其中一个是点![]() .若
.若![]() ,直接写出
,直接写出![]() 长的取值范围.(用含
长的取值范围.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
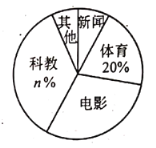
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共500棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树总金额为560000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,请你按照下面要求完成尺规作图.
,请你按照下面要求完成尺规作图.
①以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ,
,
②再分别以![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,
,
③连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
请你判断以下结论:
①![]() 是
是![]() 的一条角平分线;②连接
的一条角平分线;②连接![]() ,
,![]() 是等边三角形;③
是等边三角形;③![]() ;
;
④点![]() 在线段
在线段![]() 的垂直平分线上;⑤
的垂直平分线上;⑤![]() .其中正确的结论有________(只需要写序号).
.其中正确的结论有________(只需要写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() .
.
(1)若![]() 为
为![]() 上一动点时(如图1),
上一动点时(如图1),

①求证:![]() .
.
②试求线段![]() ,
,![]() ,
,![]() 间满足的数量关系.
间满足的数量关系.
(2)当点![]() 在
在![]() 内部时(如图2),延长
内部时(如图2),延长![]() 交
交![]() 于点
于点![]() .
.

①求证:![]() .
.
②连结![]() ,当
,当![]() 为等边三角形时,直接写出
为等边三角形时,直接写出![]() 与
与![]() 的直角边长之比.
的直角边长之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com