
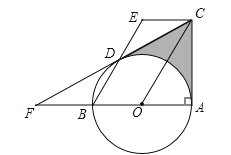
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明CF是⊙O的切线,只要证明∠CDO=90°,只要证明△COD≌△COA即可.
(2)根据条件首先证明△OBD是等边三角形,∠FDB=∠EDC=∠ECD=30°,推出DE=EC=BO=BD=OA由此根据S阴=2S△AOC﹣S扇形OAD即可解决问题.
试题解析:(1)证明:如图连接OD.
∵四边形OBEC是平行四边形,∴OC∥BE,∴∠AOC=∠OBE,∠COD=∠ODB,∵OB=OD,∴∠OBD=∠ODB,∴∠DOC=∠AOC,在△COD和△COA中,∵OC=OC,∠COD=∠COA,OD=OA,∴△COD≌△COA,∴∠CAO=∠CDO=90°,∴CF⊥OD,∴CF是⊙O的切线.
(2)解:∵∠F=30°,∠ODF=90°,∴∠DOF=∠AOC=∠COD=60°,∵OD=OB,∴△OBD是等边三角形,∴∠DBO=60°,∵∠DBO=∠F+∠FDB,∴∠FDB=∠EDC=30°,∵EC∥OB,∴∠E=180°﹣∠OBD=120°,∴∠ECD=180°﹣∠E﹣∠EDC=30°,∴EC=ED=BO=DB,∵EB=4,∴OB=OD═OA=2,在RT△AOC中,∵∠OAC=90°,OA=2,∠AOC=60°,∴AC=OAtan60°=![]() ,∴S阴=2S△AOC﹣S扇形OAD=2×
,∴S阴=2S△AOC﹣S扇形OAD=2×![]() ×2×
×2×![]() ﹣
﹣![]() =
=![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.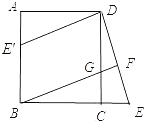
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .其中正确的个数为( )
.其中正确的个数为( ) 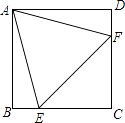
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD的外侧,以四边形的边为边分别作四个小正方形,连接相邻的两个顶点,得到四个阴影三角形,则这四个阴影三角形的面积a、b、c、d满足( ) 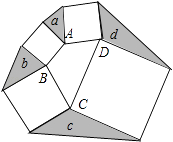
A.a+b=c+d
B.a2+b2=c2+d2
C.a+c=b+d
D.a2+c2=b2+d2
查看答案和解析>>
科目:初中数学 来源: 题型:
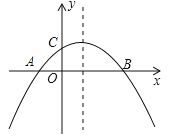
【题目】如图,二次函数![]() (
(![]() )的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②
)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②![]() ;③ac﹣b+1=0;④OAOB=
;③ac﹣b+1=0;④OAOB=![]() .
.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级进行立定跳远训练,以下是刘明和张晓同学六次的训练成绩(单位:m)
刘明:2.54,2.48,2.50,2.48,2.54,2.52
张晓:2.50,2.42,2.52,2.56,2.48,2.58
(1)填空:李明的平均成绩是 . 张晓的平均成绩是 .
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?
(3)若预知参加年级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com