
【题目】在防疫新冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用2000元购进医用口罩若干个,第二次又用2000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25倍,购进的数量比第一次少200个.
⑴求第一次和第二次分别购进的医用口罩数量为多少个?
⑵药店第一次购进口罩后,先以每个3元的价格出售,卖出了a个后购进第二批同款罩,由于进价提高了,药店将口罩的售价也提升至每个3.5元继续销售卖出了b个后,两次共收入4800元.因当地医院医疗物资紧缺,药店决定将剩余的口罩全部捐赠给医院.请问药店捐赠口罩至少有多少个?
【答案】(1)第一次和第二次分别购进的医用口罩数量为1000和800个;(2)286
【解析】
(1)设第一次购进医用口罩的数量为x个,根据题意给出的等量关系即可求出答案;
(2)由(1)可知两次购进口罩共1800个,由题意可知:3a+3.5b=4800,所以![]() ,根据条件可求出b的最小值,从而可求出药店捐赠的口罩至少有多少个.
,根据条件可求出b的最小值,从而可求出药店捐赠的口罩至少有多少个.
解:(1)设第一次购进医用口罩的数量为x个,
∴第二次购进医用口罩的数量为(x-200)个,
∴由题意可知:![]() =1.25×
=1.25×![]() ,
,
解得:x=1000,
∴x-200=800,
答:第一次和第二次分别购进的医用口罩数量为1000和800个.
(2)由(1)可知两次购进口罩共1800个,
由题意可知:3a+3.5b=4800,
∴a=1600-![]() b,
b,
∴1800-a-b=1800-(1600-![]() b)-b=200+
b)-b=200+![]() ,
,
∵a≤1000,
∴1600-![]() b≤1000,
b≤1000,
∴b≥514![]() ,
,
∵a,b是整数,
∴b是6的倍数,
∴b的最小值是516,
∴1800-a-b≥286,
答:药店捐赠口罩至少有286个.


科目:初中数学 来源: 题型:
【题目】如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点,如果∠APB在绕点P旋转时始终满足OAOB=OP2 , 我们就把∠APB叫做∠MON的关联角.
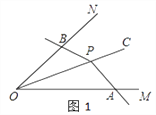
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB________∠MON的关联角(填“是”或“不是”).
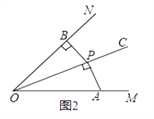
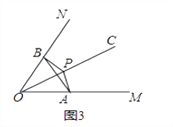
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积.
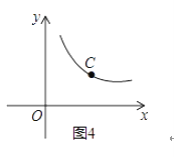
(3)如图4,点C是函数y=![]() (x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
(x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生拓展视野、丰富知识,加深与自然和文化的亲近感,增加对集体生活方式和社会公共道德的体验,我区某中学决定组织部分师生去随州炎帝故里开展研学旅行活动.在参加此次活动的师生中,若每位老师带![]() 个学生,还剩
个学生,还剩![]() 个学生没人带;若每位老师带
个学生没人带;若每位老师带![]() 个学生,就有一位老师少带
个学生,就有一位老师少带![]() 个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有
个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有![]() 名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.

(1)参加此次研学旅行活动的老师有 人;学生有 人;租用客车总数为 辆;
(2)设租用![]() 辆乙种客车,租车费用为
辆乙种客车,租车费用为![]() 元,请写出
元,请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过![]() 元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备用图甲所示的![]() 型正方形板材和
型正方形板材和![]() 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
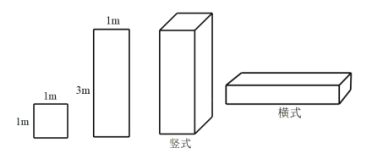
(1)若该工厂准备用不超过2400元的资金去购买![]() ,
,![]() 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知![]() 型板材每张20元,
型板材每张20元,![]() 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?
(2)若该工程新购得65张规格为![]() 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过![]() 型或
型或![]() 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2![]() .
.
①若∠C=30°,求图中阴影部分的面积;
②若![]() ,求BE的长.
,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF过平行四边形ABCD对角线的交点O,交AD于E,交BC于F,若平行四边形ABCD的周长为18,OE=1.5,则四边形EFCD的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明某天上午9时骑自行车离开家,15时回家,他离家的距离与时间的变化情况如图所示.

(1)10时时他离家 ![]() ,他到达离家最远的地方时是 时,此时离家
,他到达离家最远的地方时是 时,此时离家 ![]() ;
;
(2)他可能在哪段时间内休息,并吃午餐?
(3)他在出行途中,哪段时间内骑车速度最快,速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
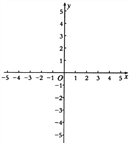
【题目】已知二次函数![]() .
.
(1)证明:不论![]() 取何值,该函数图像与
取何值,该函数图像与![]() 轴总有公共点;
轴总有公共点;
(2)若该函数的图像与![]() 轴交于点(0,3),求出顶点坐标并画出该函数图像;
轴交于点(0,3),求出顶点坐标并画出该函数图像;
(3)在(2)的条件下,观察图像,解答下列问题:
①不等式![]() 的的解集是 ;
的的解集是 ;
②若一元二次方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是 ;
的取值范围是 ;
③若一元二次方程![]() 在
在![]() 的范围内有实数根,则
的范围内有实数根,则![]() 的取
的取
值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
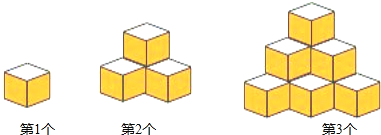
【题目】现用棱长为2cm的小立方体按如图所示规律搭建几何体,图中自上面下分别叫第一层、第二层、第三层…,其中第一层摆放1个小立方体,第二层摆放3个小立方体,第三层摆放6个小立方体…,那么搭建第1个小立方体,搭建第2个几何体需要4个小立方体,搭建第3个几何体需要10个小立方体…,按此规律继续摆放.
(1)搭建第4个几何体需要小立方体的个数为 ;
(2)为了美观,需将几何体的所有露出部分(不包含底面)都喷涂油漆,且喷涂1cm2需用油漆0.2克.
①求喷涂第4个几何体需要油漆多少克?
②如果要求从第1个几何体开始,依此对第1个几何体,第2个几何体,第3和几何体,…,第n个几何体(其中n为正整数)进行喷涂油漆,那么当喷涂完第21个几何体时,共用掉油漆多少克?
(参考公式:①1×2+2×3+3×4+…+n(n+1)=![]() ;
;
②12+22+32+…+n2=![]() ,其中n为正整数)
,其中n为正整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com