
【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
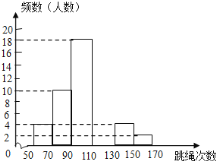
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |
科目:初中数学 来源: 题型:
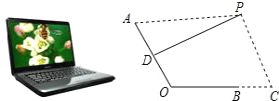
【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且![]() =
=![]() .连接AF并延长交⊙O于点E,连接AD,DE.若CF=2,AF=3.下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
.连接AF并延长交⊙O于点E,连接AD,DE.若CF=2,AF=3.下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .其中正确的是________.
.其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
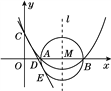
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
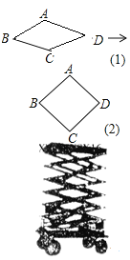
【题目】如图是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(1)如图(1)是一个基本图形,已知AB=1米,当∠ABC为60°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);
(2)当∠ABC从60°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.[结果精确到0.1米]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】C,D两城蔬菜紧缺,A,B两城决定支援,A城有蔬菜20吨,B城有蔬菜40吨,C城需要蔬菜16吨,D城需要蔬菜44吨,已知A到C,D的运输费用分别为200元/吨,220元/吨,B到C,D的运输费用分别为300元/吨,340元/吨,规定A向C城运的吨数不小于B向C城运的吨数,设A城向C城运x吨,请回答下列问题:
(1)根据题意条件,填写下列表格:

(2)设总费用为y(元),求出y(元)与x(吨)的函数关系式,并写出x的取值范围;
(3)怎样调运货物能使总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
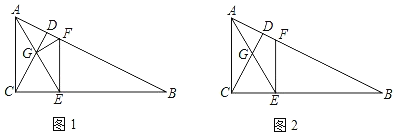
【题目】如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.
(1)求证:AE2=AFAB;
(2)连FG,若BE=2CE,求tan∠AFG;
(3)如图2,当tanB= 时,CE=FE(请直接写出结果,不需要解答过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com