
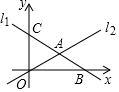
 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+8分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{3}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+8分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{3}$x交于点A.分析 (1)利用坐标轴上点的坐标特征求出点B,C坐标,联立两直线解析式确定出点A坐标;
(2)设出点M的坐标,利用三角形的面积公式建立方程即可求出点M的坐标;
(3)分两种情况即可解决问题.
解答 解:∵直线l1:y=-$\frac{1}{2}$x+8分别与x轴、y轴交于点B、C,
令x=0,则y=8,
∴C(0,8),
令y=0,则-$\frac{1}{2}$x+8=0,
∴x=16,
∴B(16,0),
联立直线l1和直线l2得,$\left\{\begin{array}{l}{y=-\frac{1}{2}x+8}\\{y=\frac{1}{3}x}\end{array}\right.$,解得,$\left\{\begin{array}{l}{x=\frac{48}{5}}\\{y=\frac{16}{5}}\end{array}\right.$,
∴A($\frac{48}{5}$,$\frac{16}{5}$),
故答案为($\frac{48}{5}$,$\frac{16}{5}$),(16,0),(0,8);
(2)∵点M在线段OA上,且直线OA的解析式为y=$\frac{1}{3}$x,设M(m,$\frac{1}{3}$m)(m>0),
∵△COM的面积为24,
∴S△COM=$\frac{1}{2}$×8×m=24,
∴m=6,
∴M(6,2),
设直线CM的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{6k+b=2}\\{b=8}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-1}\\{b=8}\end{array}\right.$,
∴直线CM的解析式为y=-x+8,
(3)如图,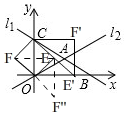
①CE是菱形的对角线时,由(2)知,直线CM的解析式为y=-x+8,
令y=0,则-x+8=0,
∴x=8,
∴E'(8,0),
∵四边形OCF'E'是菱形,
∴E'F'=OB=8,
∴∠OCE'=45°,OC=OE',
过点C作CF'∥x轴,过点E'作E'F'∥y轴相交于F',
.∴F'(8,8),
②CE为菱形的边时,∵四边形OCF'E'是菱形;
在射线CM上取一点E使CE=OC,
∵四边形OECF是菱形,
∴CE=OE,
∴点E是OC的垂直平分线,
当y=4时,-x+8=4,
∴E(4,4),
∴F(-4,4),
同理,F''(4,-4),
即:满足条件的点F的坐标为(-4,4),(4,4),(8,8).
点评 一次函数综合题,主要考查了待定系数法,三角形的面积公式,菱形的性质和判定,解本题的关键是画出图形,是一道中考常考题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (-x5)4=-x20 | B. | (a-3b)2=a2-9b2 | ||
| C. | (4xy2)2=8x2y4 | D. | (-3x+2)(-3x-2)=9x2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y=x+2与抛物线y=$\frac{1}{4}{x}^{2}$+c相交于A、B两点,若∠AOB=45°,则c的值为$\frac{\sqrt{11}}{2}$.
如图,直线y=x+2与抛物线y=$\frac{1}{4}{x}^{2}$+c相交于A、B两点,若∠AOB=45°,则c的值为$\frac{\sqrt{11}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该函数图象经过点(-1,1) | B. | 该函数图象在第二、四象限 | ||
| C. | 当x<0时,y随着x的增大而减小 | D. | 当x>1时,-1<y<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
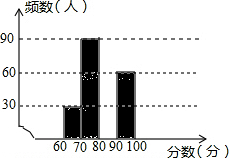 2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com