
”¾ĢāÄæ”æŅ»Į¾³ö×ā³µ“ÓAµŲ³ö·¢£¬ŌŚŅ»Ģõ¶«Ī÷×ßĻņµÄ½ÖµĄÉĻĶł·µ£¬Ćæ“ĪŠŠŹ»µÄĒéæö£Ø¼ĒĻņ¶«ĪŖÕż£©¼ĒĀ¼ČēĻĀ£Øx£¾5ĒŅx£¼14£¬µ„Ī»£ŗm£©£ŗ
ŠŠŹ»“ĪŹż | µŚŅ»“Ī | µŚ¶ž“Ī | µŚČż“Ī | µŚĖÄ“Ī |
ŠŠŹ»Ēéæö | x | © | x©3 | 2£Ø5©x£© |
ŠŠŹ»·½Ļņ£ØĢī”°¶«”±»ņ”°Ī÷”±£© | ”” ”” | ”” ”” | ”” ”” | ”” ”” |
£Ø1£©Ēė½«±ķøń²¹³äĶźÕū£»
£Ø2£©Ēó¾¹żĮ¬Šų4“ĪŠŠŹ»ŗó£¬ÕāĮ¾³ö×ā³µĖłŌŚµÄĪ»ÖĆ£»
£Ø3£©Čō³ö×ā³µŠŠŹ»µÄ×ÜĀ·³ĢĪŖ41m£¬ĒóµŚŅ»“ĪŠŠŹ»µÄĀ·³ĢxµÄÖµ£®
”¾“š°ø”æ£Ø1£©¶«£¬Ī÷£¬¶«£¬Ī÷£»£Ø2£©Ļņ¶«£Ø7©x£©km£»£Ø3£©12.
”¾½āĪö”æ
£Ø1£©øł¾ŻŹżµÄ·ūŗÅĖµĆ÷¼“æÉ£»
£Ø2£©°ŃĀ·³ĢĻą¼Ó£¬Ēó³ö½į¹ū£¬æ“½į¹ūµÄ·ūŗż“æÉÅŠ¶Ļ³ö“š°ø£»
£Ø3£©Ēó³öĆæøöŹżµÄ¾ų¶ŌÖµ£¬Ļą¼ÓĒó³ö×ÜĀ·³Ģ£¬ŌŁ½ā·½³ĢĒó½ā¼“æÉ.
½ā£ŗ£Ø1£©Ģī±ķČēĻĀ£ŗ
ŠŠŹ»“ĪŹż | µŚŅ»“Ī | µŚ¶ž“Ī | µŚČż“Ī | µŚĖÄ“Ī |
ŠŠŹ»Ēéæö | x | © | x©3 | 2£Ø5©x£© |
ŠŠŹ»·½Ļņ£ØĢī”°¶«”±»ņ”°Ī÷”±£© | ¶« | Ī÷ | ¶« | Ī÷ |
¹Ź“š°øĪŖ£ŗ¶«£¬Ī÷£¬¶«£¬Ī÷£»
£Ø2£©x+£Ø©![]() x£©+£Øx©3£©+2£Ø5©x£©=7©
x£©+£Øx©3£©+2£Ø5©x£©=7©![]() x£¬
x£¬
”ßx£¾5ĒŅx£¼14£¬
”ą7©![]() x£¾0£¬
x£¾0£¬
”ą¾¹żĮ¬Šų4“ĪŠŠŹ»ŗó£¬ÕāĮ¾³ö×ā³µĖłŌŚµÄĪ»ÖĆŹĒĻņ¶«£Ø7©x£©km£®
£Ø3£©|x|+|©![]() x|+|x©3|+|2£Ø5©x£©|=x+
x|+|x©3|+|2£Ø5©x£©|=x+![]() x+x©3©2£Ø5©x£©=
x+x©3©2£Ø5©x£©=![]() x©13£¬
x©13£¬
ŅĄĢāŅāÓŠ![]() x©13=41£¬
x©13=41£¬
½āµĆx=12£®
“š£ŗµŚŅ»“ĪŠŠŹ»µÄĀ·³ĢxµÄÖµŹĒ12£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖAB”ĪCD£¬”ĻB=40”ć£¬CNŹĒ”ĻBCEµÄĘ½·ÖĻߣ¬CM”ĶCN£¬Ēó”ĻBCMµÄ¶ČŹż£® 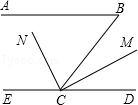
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹¤³§Ņ»ÖÜ¼Ę»®ĆæČÕÉś²śÄ³²śĘ·100¶Ö£¬ÓÉÓŚ¹¤ČĖŹµŠŠĀÖŠŻ£¬ĆæČÕÉĻ°ąČĖŹż²»Ņ»¶ØĻąµČ£¬Źµ¼ŹĆæČÕÉś²śĮæÓė¼Ę»®ĮæĻą±ČĒéæöČēĻĀ±ķ£ØŅŌ¼Ę»®ĮæĪŖ±ź×¼£¬Ōö¼ÓµÄ¶ÖŹż¼ĒĪŖÕżŹż£¬¼õÉŁµÄ¶ÖŹż¼ĒĪŖøŗŹż£©
ŠĒĘŚ | Ņ» | ¶ž | Čż | ĖÄ | Īå | Įł | ČÕ |
Ōö¼õ/¶Ö | ©1 | +3 | ©2 | +4 | +7 | ©5 | ©10 |
£Ø1£©Éś²śĮæ×ī¶ąµÄŅ»Ģģ±ČÉś²śĮæ×īÉŁµÄŅ»Ģģ¶ąÉś²ś¶ąÉŁ¶Ö£æ
£Ø2£©±¾ÖÜ×ÜÉś²śĮæŹĒ¶ąÉŁ¶Ö£æ±ČŌ¼Ę»®Ōö¼ÓĮĖ»¹ŹĒ¼õÉŁĮĖ£æŌö¼õŹżĪŖ¶ąÉŁ¶Ö£æ
£Ø3£©Čō±¾ÖÜ×ÜÉś²śµÄ²śĘ·Č«²æÓÉ35Į¾»õ³µŅ»“ĪŠŌ×°ŌŲŌĖŹäĄėæŖ¹¤³§£¬ŌņĘ½¾łĆæĮ¾»õ³µ“óŌ¼Šč×°ŌŲ¶ąÉŁ¶Ö£æ£Ø½į¹ū¾«Č·µ½0.01¶Ö£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćAµÄ×ų±źŹĒ£Ø0£¬3£©£¬µćBŌŚxÖįÉĻ£¬½«”÷AOBČʵćAÄꏱÕėŠż×Ŗ90”ćµĆµ½”÷AEF£¬µćO”¢BµÄ¶ŌÓ¦µć·Ö±šŹĒµćE”¢F£®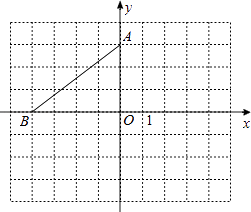
£Ø1£©ČōµćBµÄ×ų±źŹĒ£Ø©4£¬0£©£¬ĒėŌŚĶ¼ÖŠ»³ö”÷AEF£¬²¢Š“³öµćE”¢FµÄ×ų±ź£®
£Ø2£©µ±µćFĀäŌŚxÖįµÄÉĻ·½Ź±£¬ŹŌŠ“³öŅ»øö·ūŗĻĢõ¼žµÄµćBµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĄī“åŗÓÖĪĄķ¹¤³ĢŹµŃé¹ż³ĢÖŠ£¬Ä³¹¤³Ģ¶Ó½ÓŹÜŅ»ĻīæŖĶŚĖ®ĒžµÄ¹¤³Ģ£¬ĖłŠčĢģŹży£ØĢģ£©ÓėĆæĢģĶź³ÉµÄ¹¤³ĢĮæx£Øm/Ģģ£©µÄŗÆŹż¹ŲĻµĶ¼ĻóČēĶ¼ĖłŹ¾£¬ŹĒĖ«ĒśĻßµÄŅ»²æ·Ö£® 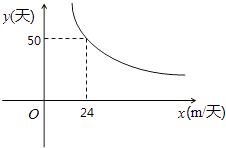
£Ø1£©Ēėøł¾ŻĢāŅā£¬ĒóyÓėxÖ®¼äµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČōøĆ¹¤³Ģ¶ÓÓŠ2ĢØĶŚ¾ņ»ś£¬ĆæĢØĶŚ¾ņ»śĆæĢģÄܹ»æŖĶŚĖ®Ēž15Ć×£¬ĪŹøĆ¹¤³Ģ¶ÓŠčÓƶąÉŁĢģ²ÅÄÜĶź³É“ĖĻīČĪĪń£æ
£Ø3£©Čē¹ūĪŖĮĖ·ĄŃ“¹¤×÷µÄ½ō¼±ŠčŅŖ£¬±ŲŠėŌŚŅ»øöŌĀÄŚ£Ø°“30Ģģ¼ĘĖć£©Ķź³ÉČĪĪń£¬ÄĒĆ“ĆæĢģÖĮÉŁŅŖĶź³É¶ąÉŁĆ×£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹Ū²ģĻĀĆęČżŠŠŹż£ŗ
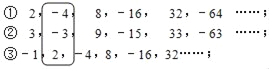
Č”ĆæŅ»ŠŠµÄµŚnøöŹż£¬ŅĄ“Ī¼ĒĪŖx”¢y”¢z£®ČēÉĻĶ¼ÖŠ£¬µ±n=2Ź±£¬x=©4£¬y=©3£¬z=2£®
£Ø1£©µ±n=7Ź±£¬ĒėÖ±½ÓŠ“³öx”¢y”¢zµÄÖµ£¬²¢ĒóÕāČżøöŹżÖŠ×ī“óµÄŹżÓė×īŠ”µÄŹżµÄ²ī£»
£Ø2£©ŅŃÖŖnĪŖżŹż£¬ĒŅx”¢y”¢zÕāČżøöŹżÖŠ×ī“óµÄŹżÓė×īŠ”µÄŹżµÄ²īĪŖ384£¬ĒónµÄÖµ£»
£Ø3£©Čōm=x+y+z£¬Ōņx”¢y”¢zÕāČżøöŹżÖŠ×ī“óµÄŹżÓė×īŠ”µÄŹżµÄ²īĪŖ”” ””£ØÓĆŗ¬mµÄŹ½×Ó±ķŹ¾£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¼×Ķ¬Ń§ŹÖÖŠ²ŲÓŠČżÕÅ·Ö±š±źÓŠŹż×Ö ![]() £¬
£¬ ![]() £¬1µÄæØʬ£¬ŅŅĶ¬Ń§ŹÖÖŠ²ŲÓŠČżÕÅ·Ö±š±źÓŠ1£¬3£¬2µÄæØʬ£¬æØʬĶāŠĪĻąĶ¬£®ĻÖ“Ó¼×ŅŅĮ½ČĖŹÖÖŠø÷ČĪČ”Ņ»ÕÅæØʬ£¬²¢½«ĖüĆĒµÄŹż×Ö·Ö±š¼ĒĪŖa£¬b£®
£¬1µÄæØʬ£¬ŅŅĶ¬Ń§ŹÖÖŠ²ŲÓŠČżÕÅ·Ö±š±źÓŠ1£¬3£¬2µÄæØʬ£¬æØʬĶāŠĪĻąĶ¬£®ĻÖ“Ó¼×ŅŅĮ½ČĖŹÖÖŠø÷ČĪČ”Ņ»ÕÅæØʬ£¬²¢½«ĖüĆĒµÄŹż×Ö·Ö±š¼ĒĪŖa£¬b£®
£Ø1£©ĒėÄćÓĆŹ÷ŠĪĶ¼»ņĮŠ±ķ·ØĮŠ³öĖłÓŠæÉÄܵĽį¹ū£®
£Ø2£©ĻÖÖʶØÕāŃłŅ»øöÓĪĻ·¹ęŌņ£ŗČōĖłŃ”³öµÄa£¬bÄÜŹ¹µĆax2+bx+1=0ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£¬Ōņ³Ę¼×»ńŹ¤£»·ńŌņ³ĘŅŅ»ńŹ¤£®ĒėĪŹÕāŃłµÄÓĪĻ·¹ęŌņ¹«Ę½Āš£æĒėÄćÓĆøÅĀŹÖŖŹ¶½āŹĶ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=ax2µÄĶ¼ĻóČēĶ¼ĖłŹ¾£¬Ōņ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģx2+x+a©1=0µÄøłµÄ“ęŌŚĒéæöŹĒ£Ø £© 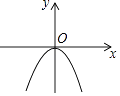
A.ƻӊŹµŹżøł
B.ÓŠĮ½øöĻąµČµÄŹµŹżøł
C.ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł
D.ĪŽ·ØČ·¶Ø
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com