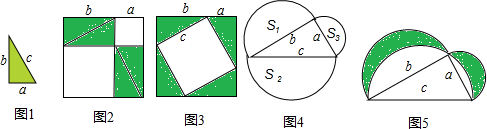
现有如图1的8张大小形状相同的直角三角形纸片,三边长分别是a、b、c.用其中4张纸片拼成如图2的大正方形(空白部分是边长分别为a和b的正方形);用另外4张纸片拼成如图3的大正方形(中间的空白部分是边长为c的正方形).
(一)观察:
从整体看,图2和图3的大正方形的面积都可以表示为(a+b)
2,结论①依据整个图形的面积等于各部分面积的和.
图2中的大正方形的面积又可以用含字母a、b的代数式表示为:
a2+b2+2ab
a2+b2+2ab
,结论②
图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为:
c2+2ab
c2+2ab
,结论③
(二)思考:
结合结论①和结论②,可以得到一个等式
(a+b)2=a2+b2+2ab
(a+b)2=a2+b2+2ab
;
结合结论②和结论③,可以得到一个等式
a2+b2=c2
a2+b2=c2
;
(三)应用:
请你运用(二)中得到的结论任意选择下列两个问题中的一个解答:
(1)求1.46
2+2×1.46×2.54+2.54
2的值;
(2)若分别以直角三角形三边为直径,向外作半圆(如图4),三个半圆的面积分别记作S
1、S
2、S
3,且S
1+S
2+S
3=20,求S
2的值.
(四)延伸(本题作为附加题,做对加2分)
若分别以直角三角形三边为直径,向上作三个半圆(如图5),直角边a=5,b=12,斜边c=13,则表示图中阴影部分面积和的数值是:
A
A
A.有理数 B.无理数 C.无法判断
请作出选择,并说明理由.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案

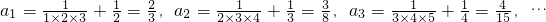 ,依据上述规律,则a99=______;
,依据上述规律,则a99=______;
 ,
, ,
, ,…,根据观察计算:
,…,根据观察计算: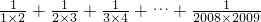 .
.