
分析 (1)通分后将${{x}_{1}}^{2}+{{x}_{2}}^{2}$变形为(x1+x2)2-2x1x2,再代入即可;
(2)按多项式乘法法则进行计算,并代入即可.
解答 解:∵方程x2-2x-1=0的两根是x1,x2,
∴x1+x2=2,x1•x2=-1,
(1)$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$;
=$\frac{{{x}_{2}}^{2}{{+x}_{1}}^{2}}{{x}_{1}{x}_{2}}$,
=-$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{1}$,
=-(-2)2+2×1,
=-4+2,
=-2;
(2)(x1-2)(x2-2).
=x1x2-2x1-2x2+4,
=-1-2(x1+x2)+4,
=-1-2×2+4,
=-1.
点评 本题考查了根与系数的关系,根据根与系数的关系,找出x1+x2=2、x1•x2=-1是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
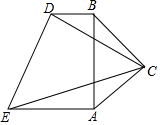 如图,在梯形AEDB中,BD∥AE,∠ABD=90°,在AB的右侧作Rt△ACB,∠ACB=90°,AC=BC,且∠ECD=45°
如图,在梯形AEDB中,BD∥AE,∠ABD=90°,在AB的右侧作Rt△ACB,∠ACB=90°,AC=BC,且∠ECD=45°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com