
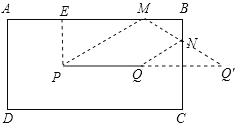
【题目】如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30,且点P到AB边的距离为3,则四边形PMNQ的周长为__.

【答案】16.
【解析】
作PE⊥AB于E,则PE=3,延长PQ、MN交于点Q',证出Q与Q'关于BC对称,MP=2PE=6,由轴对称的性质得出NQ'=NQ,证出∠Q'=30°=∠MPQ,得出MQ'=MP=6,即可得出答案.
作PE⊥AB于E,则PE=3,延长PQ、MN交于点Q',如图所示:
∵四边形ABCD是矩形,
∴∠B=90°,AB⊥BC.
∵PQ∥AB,
∴PQ⊥BC,∠EMP=∠MPQ=30°,∠Q'=∠BMN,
∴Q与Q'关于BC对称,MP=2PE=6,
∴NQ'=NQ,
由题意得:∠BMN=∠EMP=30°,
∴∠Q'=30°=∠MPQ,
∴MQ'=MP=6,
∴四边形PMNQ的周长=MP+PQ+NQ+MN=MP+PQ+NQ'+MN=MP+PQ+MQ'=6+4+6=16.
故答案为:16.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
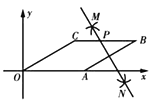
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.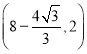 C.
C.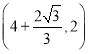 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
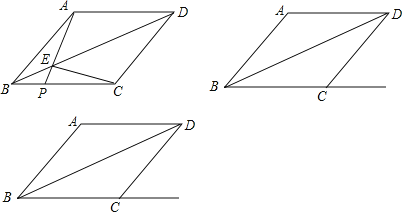
【题目】如图,菱形ABCD中,AB=10,连接BD,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
(1)求证:AE=CE;
(2)若sin∠ABD=![]() ,当点P在线段BC上时,若BP=4,求△PEC的面积;
,当点P在线段BC上时,若BP=4,求△PEC的面积;
(3)若∠ABC=45°,当点P在线段BC的延长线上时,请直接写出△PEC是等腰三角形时BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
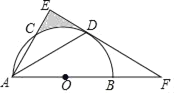
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
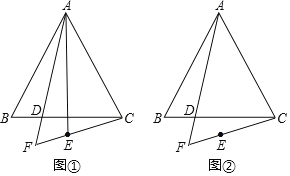
【题目】在等边△ABC中,点D是边BC上一点.作射线AD,点B关于射线AD的对称点为点E.连接CE并延长,交射线AD于点F.
(1)如图①,连接AE,
①AE与AC的数量关系是 ;
②设∠BAF=a,用a表示∠BCF的大小;
(2)如图②,用等式表示线段AF,CF,EF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图平面直角坐标系,已知二次函数![]() (m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(1)点B的坐标为 ,点D的坐标为 ;(用含有m的代数式表示)
(2)连接CD,BC.
①若![]() ,求二次函数的表达式;
,求二次函数的表达式;
②若把ABC沿着直线BC翻折,点A恰好在直线CD上,求二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
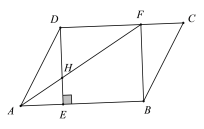
【题目】在平行四边形 ABCD 中,过点 D 作 DE⊥AB 于点 E,点 F 在 CD 上,CF =AE,连接 BF,AF.
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分∠BAD,交DE与H点,且 AB=3AE,BF=6,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
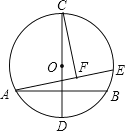
【题目】如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com