

分析 (1)由平行四边形的性质得出AB∥CD,AB=CD,再由已知条件得出AB=CE,即可得出结论;
(2)证明四边形ABEC是菱形,得出AB=BE=EC=AC,得出△ABC、△BCE、△ABE、△ACE是等腰三角形,再证出AC=CD,得出△ACD是等腰三角形.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∵CE=CD,
∴AB=CE,
∴四边形ABEC是平行四边形;
(2)解:等腰三角形有:△ABC、△BCE、△ABE、△ACE、△ACD;理由如下:
∵四边形ABEC是平行四边形,
∵AE⊥BC,
∴四边形ABEC是菱形,
∴AB=BE=EC=AC,
∴△ABC、△BCE、△ABE、△ACE是等腰三角形,
又∵四边形ABCD为平行四边形,
∴AB=CD,
∴AC=CD,
∴△ACD是等腰三角形.
点评 本题考查了平行四边形的性质与判定、菱形的判定与性质、等腰三角形的判定;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:解答题
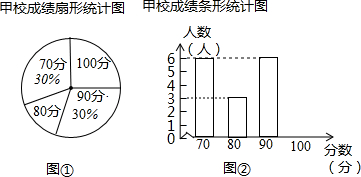 某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:| 分数(分) | 人数(人) |
| 70 | 7 |
| 80 | |
| 90 | 1 |
| 100 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线l1∥l2,A、B分别是l1、l2上的点,l3和l1、l2分别交于点C、D,点P是线段CD上的动点(点P不与C、D重合).
如图,已知直线l1∥l2,A、B分别是l1、l2上的点,l3和l1、l2分别交于点C、D,点P是线段CD上的动点(点P不与C、D重合).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1600 | 1300 |
| 售价(元/台) | 1800 | 1400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com