
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.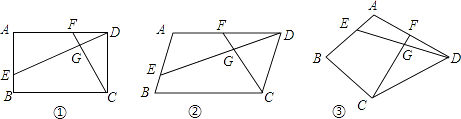
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:△ADE∽△DCF;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时, ![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出 ![]() 的值.
的值.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠ADE+∠CDG=90°,
又∵DE⊥CF,∠CDG+∠DCF=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF.
(2)
解:当∠B+∠EGC=180°时, ![]() 成立,理由如下:
成立,理由如下:
在AD的延长线上取点M,使CM=CF,如图1所示:
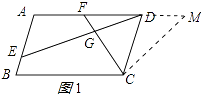
则∠CMF=∠CFM.∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A=∠CDM,∠FCB=∠CFM,
∵∠B+∠EGC=180°,
∴∠BEG+∠FCB=360°﹣(∠B+∠EGC)=180°,
又∵∠BEG+∠AED=180°,
∴∠AED=∠FCB,
∴∠CMF=∠AED.
∴△ADE∽△DCM,
∴ ![]() ,
,
∴ ![]() ;
;
(3)
解: ![]() ;理由如下:
;理由如下:
连接AC、BD,交于点M,作CN⊥AD于N,如图2所示:

∵∠BAD=90°,AB=6,AD=8,
∴BD= ![]() =
= ![]() =10,
=10,
在△ABD和△CBD中, 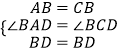 ,
,
∴△ABD≌△CBD(SAS),
∴∠ABD=∠CBD,
∵AB=CB,
∴BD⊥AC,AM=CM,
∴∠AMD=90°=∠BAD,
又∵∠ADB=∠MDA,
∴△ABD∽△MAD,
∴AD:DM=BD:AD,
∴AD2=BDDM,即82=10DM,
∴DM=6.4,
∴AM= ![]() =
= ![]() =4.8,
=4.8,
∴AC=2AM=9.6,
∵△ACD的面积= ![]() ADCN=
ADCN= ![]() ACDM,
ACDM,
∴8×CN=9.6×6.4,
解得:CN=7.68,
∵DE⊥CF,
∴∠CFN=∠DAE,
∵CN⊥AD,
∴∠CNF=90°=∠DAE,
∴△ADE∽△NCF,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由矩形的性质得出∠A=∠ADC=90°,由角的互余关系整除∠ADE=∠DCF,即可得出△ADE∽△DCF;(2)在AD的延长线上取点M,使CM=CF,由等腰三角形的性质得出∠CMF=∠CFM.由平行四边形的性质得出∠A=∠CDM,∠FCB=∠CFM,证出∠BEG+∠FCB=180°,得出∠AED=∠FCB,因此∠CMF=∠AED.证明△ADE∽△DCM,得出对应边成比例 ![]() ,即可得出结论;(3)连接AC、BD,交于点M,作CN⊥AD于N,由勾股定理求出BD,由SAS证明△ABD≌△CBD,得出∠ABD=∠CBD,由等腰三角形的性质得出AM=CM,∠AMD=90°=∠BAD,证明△ABD∽△MAD,得出对应边成比例求出DM,由勾股定理求出AM,由△ACD的面积求出CN,证明△ADE∽△NCF,得出对应边成比例,即可得出结果.
,即可得出结论;(3)连接AC、BD,交于点M,作CN⊥AD于N,由勾股定理求出BD,由SAS证明△ABD≌△CBD,得出∠ABD=∠CBD,由等腰三角形的性质得出AM=CM,∠AMD=90°=∠BAD,证明△ABD∽△MAD,得出对应边成比例求出DM,由勾股定理求出AM,由△ACD的面积求出CN,证明△ADE∽△NCF,得出对应边成比例,即可得出结果.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
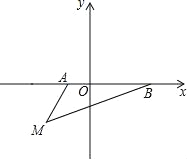
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
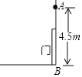
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。

(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波火车站北广场将于2015年底投入使用,计划在广场内种植A,B两种花木共6600棵,若A花木数量是B花木数量的2倍少600棵
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
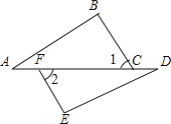
【题目】如图,已知:∠A=∠D,∠1=∠2,下列条件中能使△ABC≌△DEF的有_____.
①∠E=∠B;②ED=BC;③AB=EF;④AF=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(﹣3,0),按要求解答下列问题. 
(1)①在图中,先将△AOB向上平移6个单位,再向右平移3个单位,画出平移后的△A1O1B1;(其中点A,O,B的对应点为A1 , O1 , B1)
②在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1 , B1的对应点为A2 , B2)
(2)直接写出点A2 , B2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com