
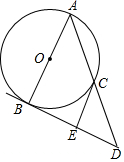
 如图,在Rt△ABC中,BC=2cm,AC=4cm,以AB长为直径作圆⊙O,过点B的切线与AC的延长线交于点D,E是BD的中点,连接CE.
如图,在Rt△ABC中,BC=2cm,AC=4cm,以AB长为直径作圆⊙O,过点B的切线与AC的延长线交于点D,E是BD的中点,连接CE.分析 连接OC,由AB为⊙O的直径知∠ACB=∠BCD=90°,从而在Rt△ABC和Rt△BCD中,根据OA=OB=OC、BE=DE知∠1=∠2、∠3=∠4,最后由BD是⊙O的切线,即∠2+∠4=90°可得∠1+∠3=90°,即可得证.
解答 证明:如图,连接OC,
∵AB为⊙O的直径,
∴∠ACB=∠BCD=90°,
在Rt△ABC和Rt△BCD中,
∵OA=OB=OC、BE=DE,
∴∠1=∠2,∠3=∠4,
∵BD是⊙O的切线,
∴∠2+∠4=90°,
∴∠1+∠3=90°,
∴CE是⊙O的切线.
点评 本题主要考查切线的判定与性质、圆周角定理及直角三角形的性质,熟练掌握切线的判定是关键:连接半径,证明半径与直线垂直.


科目:初中数学 来源: 题型:选择题
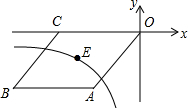 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,-4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过菱形OABC中心E点,则k的值为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )| A. | (2017,0) | B. | (2017,$\sqrt{3}$) | C. | (2017,-$\sqrt{3}$) | D. | (2016,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com