
 在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7),(-3,0),(0,3).
在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7),(-3,0),(0,3).分析 (1)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(2)直接利用平移的性质得出各对应点位置,进而得出答案;
(3)利用平移的性质得出m,n的值.
解答 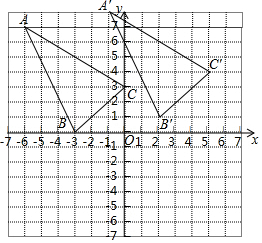 解:(1)如图所示:三角形ABC的面积为:
解:(1)如图所示:三角形ABC的面积为:
S△ABC=6×7-$\frac{1}{2}$×3×7-$\frac{1}{2}$×3×3-$\frac{1}{2}$×4×6
=42-10.5-4.5-12
=15;
(2)如图所示:△A′B′C′即为所求,A′(-1,8),B′(2,1);
故答案为:(-1,8),(2,1);
(3)∵点P(-3,m)为三角形ABC内一点,将点P向右平移4个单位后,再向下平移6个单位得到点Q(n,-3),
∴n=-3+4=1,m-6=-3,
则:m=3,n=1,
故答案为:3,1.
点评 此题主要考查了平移变换以及三角形面积求法,正确得出对应点位置是解题关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
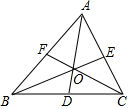 如图,D、E、F分别为△ABC各边中点,AD、BE、CF交于O点,则图中面积相等的三角形共有( )
如图,D、E、F分别为△ABC各边中点,AD、BE、CF交于O点,则图中面积相等的三角形共有( )| A. | 15对 | B. | 18对 | C. | 30对 | D. | 33对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com