
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.

(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】试题分析:(1)求出平行四边形AGCD,推出CD=AG,推出EG=DF,EG∥DF,根据平行四边形的判定推出即可;
(2)连接DG,求出∠DGC=90°,求出DF=GF,根据菱形的判定推出即可.
试题解析:(1)∵AG∥DC,AD∥BC,∴四边形AGCD是平行四边形,∴AG=DC,∵E、F分别为AG、DC的中点,∴GE=![]() AG,DF=
AG,DF=![]() DC,即GE=DF,GE∥DF,∴四边形DEGF是平行四边形;
DC,即GE=DF,GE∥DF,∴四边形DEGF是平行四边形;
(2)连接DG,∵四边形AGCD是平行四边形,∴AD=CG,∵G为BC中点,∴BG=CG=AD,∵AD∥BG,∴四边形ABGD是平行四边形,∴AB∥DG,∵∠B=90°,∴∠DGC=∠B=90°,∵F为CD中点,∴GF=DF=CF,即GF=DF,∵四边形DEGF是平行四边形,∴四边形DEGF是菱形.



科目:初中数学 来源: 题型:
【题目】如图,在数轴上点 A 表示的有理数为﹣4,点 B 表示的有理数为 6,点 P 从 点 A 出发以每秒 2 个单位长度的速度在数轴上沿由 A 到 B 方向运动,当点 P 到 达点 B 后立即返回,仍然以每秒 2 个单位长度的速度运动至点 A 停止运动.设 运动时间为 t(单位:秒).
(1)求 t=2 时点 P 表示的有理数;
(2)求点 P 是 AB 的中点时 t 的值;
(3)在点 P 由点 A 到点 B 的运动过程中,求点 P 与点 A 的距离(用含 t 的代数式表示);
(4)在点 P 由点 B 到点 A 的返回过程中,点 P 表示的有理数是多少(用含 t 的 代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,直线
,直线![]() ,垂足为O,直线PQ经过点O,且
,垂足为O,直线PQ经过点O,且![]() 点B在直线l上,位于点O下方,
点B在直线l上,位于点O下方,![]() 点C在直线PQ上运动
点C在直线PQ上运动![]() 连接BC过点C作
连接BC过点C作![]() ,交直线MN于点A,连接
,交直线MN于点A,连接![]() 点A、C与点O都不重合
点A、C与点O都不重合![]() .
.
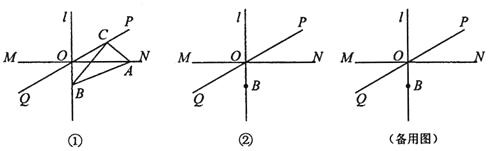
![]() 小明经过画图、度量发现:在
小明经过画图、度量发现:在![]() 中,始终有一个角与
中,始终有一个角与![]() 相等,这个角是________________;
相等,这个角是________________;
![]() 当
当![]() 时,在图
时,在图![]() 中画出示意图并证明
中画出示意图并证明![]() ;
;
![]() 探索
探索![]() 和
和![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
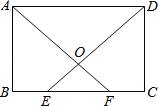
【题目】(10分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .
项目品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
A | 800 | x |
|
B | 1000 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG,AE.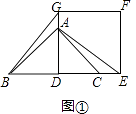
(1)求证:BG=AE;
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)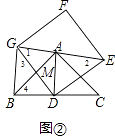
①求证:BG⊥GE;
②设DG与AB交于点M,若AG:AE=3:4,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com