
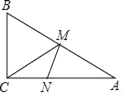
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=4,M是AB边上一动点,N是AC边上的一动点,则MN+MC的最小值为_____.
科目:初中数学 来源: 题型:
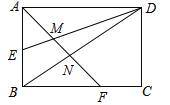
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.

(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
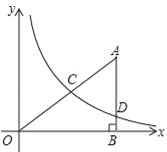
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家环保局统一规定:空气质量分为5级,当空气污染指数达![]() 为1级,质量为优;
为1级,质量为优;![]() 时为2 级,质量为良;
时为2 级,质量为良;![]() 时为3级,轻度污染;
时为3级,轻度污染;![]() 时为4级,中度污染;300以上时为5级,重度污染。某城市随机抽取了2019年某些天的空气质量检测结果,并整理绘制成如下两端不完整的统计图。请根据图中信息,解答下列各题。
时为4级,中度污染;300以上时为5级,重度污染。某城市随机抽取了2019年某些天的空气质量检测结果,并整理绘制成如下两端不完整的统计图。请根据图中信息,解答下列各题。
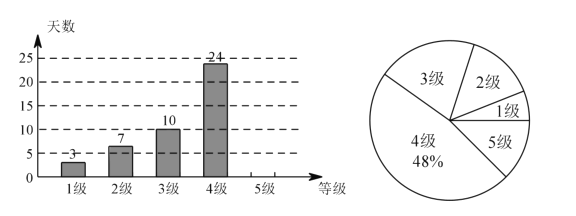
(1)本次调查共抽取了________天的空气质量检测结果进行统计。
(2)补全条形统计图。
(3)扇形统计图中3级空气质量所对应的圆心角为______度。
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2019年该城市有多少天不适宜开展户外活动。(2019年,共365天)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:( )
①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DAE,其中结论正确的个数有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题:
(1)求图中的a值;
(2)若在距离小明家5千米处有一个地点C,小明从第一层经过点C到第二层经过点C,所用时间为1.75小时,求小明返回过程中,s与t的函数解析式,不必写出自变量的取值范围;
(3)在(2)的条件下,求小明从出发到回到家所用的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备在国庆节期间组织学生到泰山进行研学旅行,已知老师与学生一共25人参加此次研学旅行,购买门票共花费1700元,门票费用如表格所示,求参加研学旅行的老师和学生各有多少人?设老师有x人,学生有y人,则可列方程组为( )
景点 | 票价 | 开放时间 |
泰山门票 | 旺季:125元/人 淡季:100元/人 | 全天 |
说明:(1)旺季时间(2月~11月),淡季时间(12月-次年1月); (2)老年人(60岁~70岁)、学生、儿童(1.2米~1.4米)享受5折优惠; (3)教师、省部级劳模、英模、道德模范享受8折优惠; (4)现役军人、伤残军人、70岁以上老年人、残疾人,凭本人有效证件免费进山; (5)享受优惠的游客请出示本人有效证件。 | ||
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com