
【题目】如图,线段 AB=24,动点 P 从 A 出发,以每秒 2 个单位的速度沿射线 AB运动,运动时间为 t 秒(t>0),M 为 AP 的中点.
(1)当点 P 在线段 AB 上运动时,
①当 t 为多少时,PB=2AM?②求2BM-BP的值.
(2)当 P 在 AB 延长线上运动时,N 为 BP 的中点,说明线段 MN 的长度不变,并 求出其值.
(3)在 P 点的运动过程中,是否存在这样的 t 的值,使 M、N、B 三点中的一个点 是以其余两点为端点的线段的中点,若有,请求出 t 的值;若没有,请说明理 由.
![]()
【答案】(1)①6②24(2)12(3)18或36
【解析】试题分析:(1)①分两种情况讨论:点P在点B左边;点P在点B右边,分别求出t的值即可;
②AM=x,BM=24﹣x,PB=24﹣2x,表示出2BM﹣BP后,化简即可得出结论;
(2)PA=2x,AM=PM=x,PB=2x﹣24,PN=![]() PB=x﹣12,表示出MN的长度,即可得到结论;
PB=x﹣12,表示出MN的长度,即可得到结论;
(3)分三种情况讨论:①当P在线段AB上时;②当P在线段AB的延长线上,M在线段AB上时;③当P和M都在线段AB的延长线上时.
试题解析:解:(1)①设出发x秒后PB=2AM,当点P在点B左边时,PA=2x,PB=24﹣2x,AM=x,由题意得:24﹣2x=2x,解得:x=6;
当点P在点B右边时,PA=2x,PB=2x﹣24,AM=x,由题意得:2x﹣24=2x,方程无解.
综上所述:出发6秒后PB=2AM.
②∵AM=x,BM=24﹣x,PB=24﹣2x,∴2BM﹣BP=2(24﹣x)﹣(24﹣2x)=24;
(2)∵PA=2x,AM=PM=x,PB=2x﹣24,PN=![]() PB=x﹣12,∴MN=PM﹣PN=x﹣(x﹣12)=12(定值);
PB=x﹣12,∴MN=PM﹣PN=x﹣(x﹣12)=12(定值);
(3)①当P在线段AB上时,如图1,有AP=2t,BP=24-2t,AM=MP=t,PN=NB=12-t,MN=12.若MN=NB,则12=12-t,解得t=0,不合题意,舍去.

②当P在线段AB的延长线上,M在线段AB上时,如图2,有AP=2t,BP=2t-24,AM=MP=t,MB=24-t, PN=NB=t-12.若MB=NB,则24-t=t-12,解得t=18.

③当P和M都在线段AB的延长线上时,如图3,有AP=2t,BP=2t-24,AM=MP=t,MB=t-24, PN=NB=t-12,MN=BN-BM=t-12-(t-24)=12.若MB=MN,则t-24= 12,解得t=36.
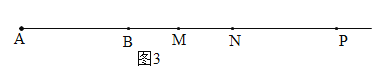
综上所述:t=18或36.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.

(1)试说明:DE=DF;
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明所归纳结论;
(3)若题中条件“∠CAB=60°,∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.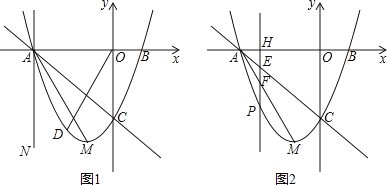
(1)填空:b= , c= , 直线AC的解析式为
(2)直线x=t与x轴相交于点H.
①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为 ![]() ,求此时t的值.
,求此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量y1(万m3)与干旱持续时间x(天)的关系如图中线段l1所示,针对这种干旱情况,从第20天开始向水库注水,注水量y2(万m3)与时间x(天)的关系如图中线段l2所示(不考虑其它因素).
(1)求原有蓄水量y1(万m3)与时间x(天)的函数关系式,并求当x=20时的水库总蓄水量.
(2)求当0≤x≤60时,水库的总蓄水量y(万m3)与时间x(天)的函数关系式(注明x的范围),若总蓄水量不多于900万m3为严重干旱,直接写出发生严重干旱时x的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列题目.
![]() 求:
求:![]() 的值.
的值.
对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成![]() 的形式,而
的形式,而![]() ,这样就把
,这样就把![]() 一项
一项![]() 分
分![]() 裂成了两项.
裂成了两项.
试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出![]() 的值.
的值.
![]() 若
若![]()
![]() 求:A、B的值:
求:A、B的值:
![]() 求:
求:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=![]() S四边形ABCD;⑤BC=CE.( )
S四边形ABCD;⑤BC=CE.( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:
请根据以上信息,解答下列问题:
(1)全体参赛的学生共有人,“建模”在扇形统计图中的圆心角是°;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com