
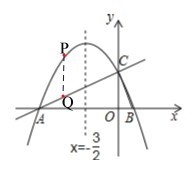
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)PAC的面积有最大值是4,此时,P(-2,3);(3)存在,
;(2)PAC的面积有最大值是4,此时,P(-2,3);(3)存在,![]()
【解析】
(1)根据待定系数法,即可得到答案;
(2)设P![]() ,过点P作PQ⊥x轴交AC于点Q,则点Q
,过点P作PQ⊥x轴交AC于点Q,则点Q![]() ,根(3)根据三角形的面积公式,得到二次函数解析式,即可得到答案;
,根(3)根据三角形的面积公式,得到二次函数解析式,即可得到答案;
设![]() ,则
,则![]() ,若以点A、M、N为顶点的三角形与△ABC相似,则
,若以点A、M、N为顶点的三角形与△ABC相似,则![]() 或
或![]() ,分别求出t的值,即可得到答案.
,分别求出t的值,即可得到答案.
(1)∵直线y=![]() x+2与x轴交于点A,与y轴交于点C,
x+2与x轴交于点A,与y轴交于点C,
∴A(-4,0),C(0,2)
∵抛物线y=ax2+bx+c的对称轴是x=![]() 且过A(-4,0),C(0,2),
且过A(-4,0),C(0,2),
∴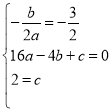 ,解得:
,解得: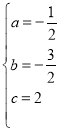
∴抛物线解析式为:![]() ;
;
(2)设P![]() ,
,
过点P作PQ⊥x轴交AC于点Q,如图,
∴点Q![]() ,
,
∴PQ=![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴当m=-2时,PAC的面积有最大值是4,此时,P(-2,3);
(3)∵![]() ,
,
∴A(-4,0),C(0,2)B(1,0),
∴AB=5,AC=2![]() ,BC=
,BC=![]() ,
,
∵![]() ,
,
∴AC⊥BC,
∵MN ⊥x轴,
∴若以点A、M、N为顶点的三角形与△ABC相似,则![]() 或
或![]() ,
,
设![]() ,则
,则![]() ,
,
①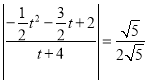 ,
,
∴![]() ,解得:
,解得:![]()
②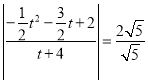 ,
,
∴![]() ,解得:
,解得:![]()
综上所述:存在![]() 使得以点A、M、N为顶点的三角形与△ABC相似.
使得以点A、M、N为顶点的三角形与△ABC相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD=5cm, AP=8cm , AP平分∠DAB,交DC于点P,过点B作BE⊥AD于点E,BE交AP于点F,则tan∠BFP= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 的顶点为
的顶点为![]() ,它与
,它与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 左侧).
左侧).
(![]() )求点
)求点![]() 、点
、点![]() 的坐标;
的坐标;
(![]() )将这个抛物线的图象沿
)将这个抛物线的图象沿![]() 轴翻折,得到一个新抛物线,这个新抛物线与直线
轴翻折,得到一个新抛物线,这个新抛物线与直线![]() 交于点
交于点![]() .
.
①求证:点![]() 是这个新抛物线与直线
是这个新抛物线与直线![]() 的唯一交点;
的唯一交点;
②将新抛物线位于![]() 轴上方的部分记为
轴上方的部分记为![]() ,将图象
,将图象![]() 以每秒
以每秒![]() 个单位的速度向右平移,同时也将直线
个单位的速度向右平移,同时也将直线![]() 以每秒
以每秒![]() 个单位的速度向上平移,记运动时间为
个单位的速度向上平移,记运动时间为![]() ,请直接写出图象
,请直接写出图象![]() 与直线
与直线![]() 有公共点时运动时间
有公共点时运动时间![]() 的范围.
的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面材料,然后解决问题:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:![]() ,
,![]() ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:![]() ,
,![]() .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如:![]() =2+
=2+![]() =2
=2![]() ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:![]() =1+
=1+![]() .
.
(1)将分式![]() 化为带分式;
化为带分式;
(2)当x取哪些整数值时,分式![]() 的值也是整数?
的值也是整数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,1),B(-1,1),C(0,4).
(1)在平面直角坐标系中描出A,B,C三点;
(2)在同一平面内,点与三角形的位置关系有三种:点在三角形内、点在三角形边上、 点在三角形外.若点P在△ABC外,请判断点P关于y轴的对称点P′与△ABC的位置关系,直接写出判断结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潼南中学有一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子![]() ,
,![]() 恰在水面中心,安置在柱子顶端
恰在水面中心,安置在柱子顶端![]() 处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过
处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过![]() 的任一平面上,抛物线形状如图
的任一平面上,抛物线形状如图![]() 所示.图
所示.图![]() 建立直角坐标系,水流喷出的高度
建立直角坐标系,水流喷出的高度![]() (米)与水平距离
(米)与水平距离![]() (米)之间的关系是
(米)之间的关系是![]() .请问:若不计其他因素,水池的半径至少要________米才能使喷出的水流不至于落在池外.
.请问:若不计其他因素,水池的半径至少要________米才能使喷出的水流不至于落在池外.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com