
【题目】如图所示:两个同心圆,半径分别是![]() 和
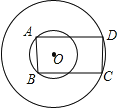
和![]() ,矩形ABCD边AB,CD分别为两圆的弦,当矩形ABCD面积取最大值时,矩形ABCD的周长是_____.
,矩形ABCD边AB,CD分别为两圆的弦,当矩形ABCD面积取最大值时,矩形ABCD的周长是_____.
【答案】16+12![]() .
.
【解析】
根据锐角三角函数的概念可以证明三角形的面积等于相邻两边的乘积乘以夹角的正弦值,根据这一公式分析面积的最大值的情况.然后运用勾股定理、以及直角三角形的斜边上的高等于两条直角边的乘积除以斜边求得长方形的长和宽,进一步求得其周长.
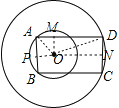
解:连接OA,OD,作OP⊥AB于P,OM⊥AD于M,ON⊥CD于N.
根据矩形的面积以及三角形的面积公式发现:矩形的面积是三角形AOD的面积的4倍.
因为OA,OD的长是定值,则∠AOD的正弦值最大时,三角形的面积最大,即∠AOD=90°,则AD=6![]() ,根据三角形的面积公式求得OM=4,即AB=8.
,根据三角形的面积公式求得OM=4,即AB=8.
则矩形ABCD的周长是16+12![]() .
.


科目:初中数学 来源: 题型:
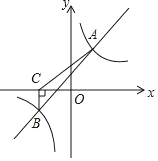
【题目】如图所示,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
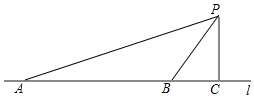
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速,如图新建的醴陵320国道(用直线l表示),进入株洲城区的AB路段设有区间测速,所有车辆限速60千米/小时(约为16.7米/秒),数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=40米,∠APC=71°,∠BPC=35°.
(1)求AB的长;
(2)若上午9时测得一汽车从点A到点B用时5.5秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
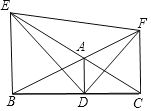
【题目】如图,从△ABC各顶点作平行线AD∥EB∥FC,各与其对边或其延长线相交于D,E,F.若△ABC的面积为1,则△DEF的面积为( )
A.3B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.

(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
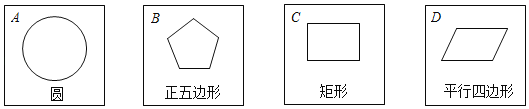
【题目】有四张反面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.
,其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.
(1)从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是 .
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸牌用![]() 表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.
表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点M(3,2),抛物线L:y=x2﹣3x+c与x轴从左到右的交点为A,B.
(1)若抛物线L经过点M(3,2),求抛物线L的解析式和顶点坐标;
(2)当2OA=OB时,求c的值;
(3)直线y=x+b经过点M,与y轴交于点N,①求点N的坐标;②若线段MN与抛物线L:y=x2﹣3x+c有唯一公共点,直接写出正整数c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com