
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼¢Ł£¬ŌŚRt”÷ABCÖŠ£¬”ĻABC=90”ć£¬BD”ĶACÓŚµćD£¬ĒŅAB=5£¬AD=4£¬ŌŚADÉĻČ”Ņ»µćG£¬Ź¹AG=![]() £¬µćPŹĒÕŪĻßCB©BAÉĻŅ»¶Æµć£¬ŅŌPGĪŖÖ±¾¶×÷”ŃO½»ACÓŚµćE£¬Į¬½įPE£®
£¬µćPŹĒÕŪĻßCB©BAÉĻŅ»¶Æµć£¬ŅŌPGĪŖÖ±¾¶×÷”ŃO½»ACÓŚµćE£¬Į¬½įPE£®
£Ø1£©ĒósinCµÄÖµ£»
£Ø2£©µ±µćPÓėµćBÖŲŗĻŹ±ČēĶ¼¢ŚĖłŹ¾£¬”ŃO½»±ßABÓŚµćF£¬ĒóÖ¤£ŗ”ĻEPG=”ĻFPG£»
£Ø3£©µćPŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠ£ŗ
¢Łµ±BC»ņABÓė”ŃOĻąĒŠŹ±£¬ĒóĖłÓŠĀś×ćĢõ¼žµÄDE³¤£»
¢ŚµćPŅŌŌ²ŠÄOĪŖŠż×ŖÖŠŠÄ£¬Ė³Ź±Õė·½ĻņŠż×Ŗ90”ćµĆµ½P”䣬µ±P”äĒ”ŗĆĀäŌŚAB±ßÉĻŹ±£¬Ēó”÷OPP”äÓė”÷OGEµÄĆ껿֮±Č£ØĒėÖ±½ÓŠ“³ö“š°ø£©£®

”¾“š°ø”æ£Ø1£©sin”ĻC=![]() £»£Ø2£©Ö¤Ć÷¼ū½āĪö£»£Ø3£©¢ŁDE³¤ĪŖ
£»£Ø2£©Ö¤Ć÷¼ū½āĪö£»£Ø3£©¢ŁDE³¤ĪŖ![]() »ņ
»ņ![]() »ņ
»ņ![]() £»¢ŚĀś×ćĢõ¼žµÄ”÷OPP”äÓė”÷OGEµÄĆ껿֮±ČĪŖ25£ŗ24»ņ25£ŗ7£®
£»¢ŚĀś×ćĢõ¼žµÄ”÷OPP”äÓė”÷OGEµÄĆ껿֮±ČĪŖ25£ŗ24»ņ25£ŗ7£®
”¾½āĪö”æ
£Ø1£©Ņ×Ö¤”ĻC=”ĻABD£¬Ōņsin”ĻC=sin”ĻABD=![]() =
=![]() £»
£»
£Ø2£©Į¬½ÓCF£¬øł¾ŻŌ²ÖܽĒ¶ØĄķµĆ”ĻBFG=”ĻAFG=90”ć£¬ŌņsinA=![]() £¬æÉĒóµĆFG=
£¬æÉĒóµĆFG=![]() £¬ŌŁĒó³öDG=AD©AG=4©
£¬ŌŁĒó³öDG=AD©AG=4©![]() =
=![]() £¬ŌņFG=DG£¬¼“æɵĆÖ¤£»
£¬ŌņFG=DG£¬¼“æɵĆÖ¤£»
£Ø3£©¢Ł”ŃOÓėABĻąĒŠÓŠĮ½ÖÖĒéæö£¬ÓėBCĻąĒŠÓŠŅ»ÖÖĒéæö£¬ČēĶ¼3”¢4”¢5£¬Įé»īŌĖÓĆĒŠĻߵĊŌÖŹ£¬Čż½ĒŗÆŹżÓė¹“¹É¶ØĄķ·Ö±šĒó½ā¼“æÉ£»
¢ŚČēĶ¼3ÖŠ£¬ÓĆ£Ø2£©æÉÖŖ£¬µćPŅŌŌ²ŠÄOĪŖŠż×ŖÖŠŠÄ£¬Ė³Ź±Õė·½ĻņŠż×Ŗ90”ćµĆµ½P£¬
µ±PĒ”ŗĆĀäŌŚAB±ßÉĻŹ±£¬“ĖŹ±”÷OPP”äÓė”÷OGEµÄĆ껿֮±Č=![]() ”Į
”Į![]() ”Į
”Į![]() £ŗ
£ŗ![]() ”Į
”Į![]() ”Į
”Į![]() ”Į
”Į![]() =25£ŗ24£»
=25£ŗ24£»
ČēĶ¼6ÖŠ£¬µ±”÷POHŹĒµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬Į¬½ÓPE£¬ĄūÓĆĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒóµĆAE=![]() £¬PE=
£¬PE=![]() £¬¼“GE=AE©AG=
£¬¼“GE=AE©AG=![]() £¬Ōņ”÷OPP”äÓė”÷OGEµÄĆ껿֮±Č=
£¬Ōņ”÷OPP”äÓė”÷OGEµÄĆ껿֮±Č=![]() ”Į
”Į![]() ”Į
”Į![]() £ŗ
£ŗ![]() ”Į
”Į![]() ”Į
”Į![]() ”Į
”Į![]() =25£ŗ7.
=25£ŗ7.
£Ø1£©”ßBD”ĶAC£¬
”ą”ĻADB=90”ć£¬
”ß”ĻABC=90”ć£¬
”ą”ĻC+”ĻA=90”ć£¬”ĻA+”ĻABD=90”ć£¬
”ą”ĻA=”ĻABD£¬
”ąsin”ĻC=sin”ĻABD=![]() =
=![]() £»
£»
£Ø2£©ČēĶ¼2ÖŠ£¬Į¬½ÓGF,
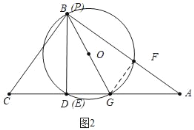
ŌŚRt”÷ABDÖŠ£¬BD=![]() =3£¬
=3£¬
”ßBGŹĒÖ±¾¶£¬
”ą”ĻBFG=”ĻAFG=90”ć£¬
”ąsinA=![]() £¬¼“
£¬¼“![]() £¬
£¬
”ąFG=![]() £¬
£¬
”ßDG=AD©AG=4©![]() =
=![]() £¬
£¬
”ąGD=GF£¬
”ą”ĻEPG=”ĻFPG£»
£Ø3£©¢ŁČēĶ¼3ÖŠ£¬µ±”ŃOÓėBCĻąĒŠŹ±£¬×÷OH”ĶABÓŚH£¬
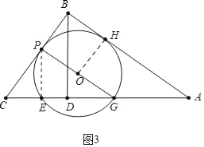
”ß”ĻOPB=”ĻPBH=”ĻOHB=90”ć£¬
”ąĖıߊĪPBHOŹĒ¾ŲŠĪ£¬
”ß”ĻC+”ĻA=90”ć£¬”ĻDBA+”ĻA=90”ć£¬
”ą”ĻC=”ĻABD£¬”ß”ĻBDC=”ĻBDA£¬
”ą”÷BDC”×”÷ADB£¬
”ąBD2=CDAD£¬
”ąCD=![]() £¬
£¬
”ąBC=![]() =
=![]() £¬
£¬
”ßBCŹĒĒŠĻߣ¬
”ąGP”ĶBC£¬
”ąGPC=”ĻABC=90”ć£¬
”ąGP”ĪAB£¬
”ą”ĻCGP=”ĻA£¬
”ąsin”ĻA=sin”ĻPGC£¬
”ą![]() £¬¼“
£¬¼“![]() £¬
£¬
”ąPC=![]() £¬
£¬
”ąPB=BC©PC=![]() £¬
£¬
”ąPG=![]() =3£¬
=3£¬
”ąOH=PB=![]() £¬
£¬
”ą“ĖŹ±”ŃOÓėABĻąĒŠ£¬Į¬½ÓPE£¬
”ßPGŹĒ”ŃOµÄÖ±¾¶£¬
”ą”ĻPEG=90”ć£¬
”ą”ĻPEC=”ĻCDB=90”ć£¬
”ąPE”ĪBD£¬
”ąDE£ŗCD=PB£ŗBC£¬
”ąDE£ŗ![]() =
=![]() £ŗ
£ŗ![]() £¬
£¬
”ąDE=![]() £»
£»
ČēĶ¼4ÖŠ£¬µ±µćPŌŚABÉĻ£¬”ŃOÓėBCĻąĒŠŹ±£¬ÉčĒŠµćĪŖT£¬Į¬½ÓOT£¬GH£¬ŃÓ³¤TO½»GHÓŚN£¬Į¬½ÓPE£¬
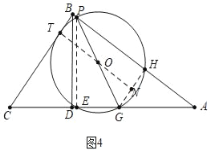
Ņ×Ö¤ĖıߊĪBTNHŹĒ¾ŲŠĪ£¬
ÓÉ£Ø1£©æÉÖŖ£ŗGH=![]() £¬AH=2£¬BH=3£¬GN=NH=
£¬AH=2£¬BH=3£¬GN=NH=![]() £¬ÉčOT=OG=m£¬
£¬ÉčOT=OG=m£¬
ŌŚRt”÷OGNÖŠ£¬”ßOG2=ON2+GN2£¬
”ąm2=£Ø3©m£©2+£Ø![]() £©2£¬
£©2£¬
”ąm=![]() £¬
£¬
”ąON=![]() £¬
£¬
”ßOG=OP£¬GN=NH£¬
”ąPH=2ON=![]() £¬
£¬
”ąPA=PH+AH=![]() £¬
£¬
”ßPE”ĪBD£¬
”ą![]() =
=![]() £¬¼“
£¬¼“![]() =
=![]() £¬
£¬
”ąAE=![]() £¬
£¬
”ąDE=AD©AE=4©![]() =
=![]() £»
£»
ČēĶ¼5ÖŠ£¬µ±”ŃOÓėABĻąĒŠŹ±£¬GP”ĶAB£¬Į¬½ÓPH£¬
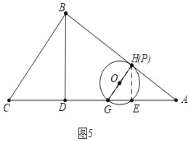
”ßHE”ĶAG£¬
”ą”ĻPEG=”ĻAPG=90”ć£¬”ß”ĻAGP=”ĻPGE£¬
”ą”÷PGE”×”÷AGH£¬
”ąPG2=GEGA£¬
”ąGE=![]() £¬
£¬
”ąDE=DG+GE=![]() +
+![]() =
=![]() £»
£»
×ŪÉĻĖłŹö£¬µ±BC»ņABÓė”ŃOĻąĒŠŹ±£¬Āś×ćĢõ¼žµÄDE³¤ĪŖ![]() »ņ
»ņ![]() »ņ
»ņ![]() £»
£»
¢ŚČēĶ¼3ÖŠ£¬ÓĆ£Ø2£©æÉÖŖ£¬µćPŅŌŌ²ŠÄOĪŖŠż×ŖÖŠŠÄ£¬Ė³Ź±Õė·½ĻņŠż×Ŗ90”ćµĆµ½P£¬
µ±PĒ”ŗĆĀäŌŚAB±ßÉĻŹ±£¬
“ĖŹ±”÷OPP”äÓė”÷OGEµÄĆ껿֮±Č=![]() ”Į
”Į![]() ”Į
”Į![]() £ŗ
£ŗ![]() ”Į
”Į![]() ”Į
”Į![]() ”Į
”Į![]() =25£ŗ24£»
=25£ŗ24£»
ČēĶ¼6ÖŠ£¬µ±”÷POHŹĒµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬Āś×ćĢõ¼ž£»
Į¬½ÓPE£¬
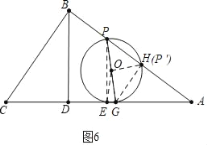
”ßPH=GH=![]() £¬AH=2£¬
£¬AH=2£¬
”ąPA=![]() £¬OP=OH=
£¬OP=OH=![]() £¬
£¬
”ßPE”ĪBD£¬
”ąPA£ŗAB=AE£ŗAD=PE£ŗBD£¬
”ą![]() £ŗ5=AE£ŗ4=PE£ŗ3£¬
£ŗ5=AE£ŗ4=PE£ŗ3£¬
”ąAE=![]() £¬PE=
£¬PE=![]() £¬
£¬
”ąGE=AE©AG=![]() £¬
£¬
”ą”÷OPP”äÓė”÷OGEµÄĆ껿֮±Č=![]() ”Į
”Į![]() ”Į
”Į![]() £ŗ
£ŗ![]() ”Į
”Į![]() ”Į
”Į![]() ”Į
”Į![]() =25£ŗ7£»
=25£ŗ7£»
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄ”÷OPP”äÓė”÷OGEµÄĆ껿֮±ČĪŖ25£ŗ24»ņ25£ŗ7£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”ĻAOB£½45£¬”ĻAOBÄŚÓŠŅ»¶ØµćP£¬ĒŅOP£½10£®ŌŚOAÉĻÓŠŅ»¶ÆµćQ£¬OBÉĻÓŠŅ»¶ÆµćR£®Čō¦¤PQRÖܳ¤×īŠ”£¬Ōņ×īŠ”Öܳ¤ŹĒ£Ø£©

A. 10 B. ![]() C. 20 D.
C. 20 D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬”ĻC£½90”ć£¬BC£½5£®
¢Å ĄūÓĆÖ±³ßŗĶŌ²¹ęŌŚAB±ßÉĻĒó×÷Ņ»µćP£¬Ź¹µĆ”ĻAPC£«”ĻBCP£½90”ć£¬²¢ĖµĆ÷ĄķÓÉ£»£Ø²»Š“×÷·Ø£¬±£Įō×÷Ķ¼ŗŪ¼££©
¢Ę ŌŚ¢ÅµÄĢõ¼žĻĀ£¬ŹŌÅŠ¶Ļ”ĻPCBÓė”ĻAÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ³¤·½ŠĪABCDÖŠ£¬AB£½6£¬AD£½9£¬ŃÓ³¤BCµ½E£¬Ź¹CE£½3£¬Į¬½ÓDE.¶ÆµćP“ÓµćB³ö·¢£¬ŅŌĆæĆė3øöµ„Ī»µÄĖŁ¶ČŃŲBC”śCD”śDAĻņÖÕµćAŌĖ¶Æ£¬ÉčµćPŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬µ±tĪŖ______ĆėŹ±£¬ŅŌP”¢A”¢BČżµć¹¹³ÉµÄČż½ĒŠĪŗĶ”÷DCEČ«µČ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
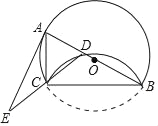
”¾ĢāÄæ”æČēĶ¼£¬ŅŌABĪŖÖ±¾¶×÷”ŃO£¬µćCĪŖ”ŃOÉĻŅ»µć£¬ĮÓ»”CBŃŲBC·ÕŪ£¬½»ABÓŚµćD£¬¹żA×÷”ŃOµÄĒŠĻß½»DCµÄŃÓ³¤ĻßÓŚµćE£®
£Ø1£©ĒóÖ¤£ŗAC=CD£»
£Ø2£©ŅŃÖŖtanE=![]() £¬AC=2£¬Ēó”ŃOµÄ°ė¾¶£®
£¬AC=2£¬Ēó”ŃOµÄ°ė¾¶£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻÖÓŠŅ»ÕÅĪå±ßŠĪµÄøÖ°åABCDEČēĶ¼ĖłŹ¾£¬”ĻA=”ĻB=”ĻC=90”ć£¬ĻÖŌŚAB±ßÉĻČ”Ņ»µćP£¬·Ö±šŅŌAP£¬BPĪŖ±ßø÷¼ōĻĀŅ»øöÕż·½ŠĪøÖ°åÄ£ŠĶ£¬Ėł¼ōµĆµÄĮ½øöÕż·½ŠĪĆ껿ŗĶµÄ×ī“óÖµĪŖ_____m2£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŌABĪŖÖ±¾¶×÷”ŃO£¬µćCĪŖ”ŃOÉĻŅ»µć£¬ĮÓ»”CBŃŲBC·ÕŪ£¬½»ABÓŚµćD£¬¹żA×÷”ŃOµÄĒŠĻß½»DCµÄŃÓ³¤ĻßÓŚµćE£®
£Ø1£©ĒóÖ¤£ŗAC=CD£»
£Ø2£©ŅŃÖŖtanE=![]() £¬AC=2£¬Ēó”ŃOµÄ°ė¾¶£®
£¬AC=2£¬Ēó”ŃOµÄ°ė¾¶£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
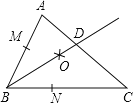
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻABC£½64”ć£¬BC”ŁAB.Š”»Ŗøł¾ŻĻĀĮŠµÄ×÷·ØŌŚ”÷ABCÉĻ×÷Ķ¼£¬ČēĶ¼ĖłŹ¾.°“ŅŖĒóĶź³ÉĻĀĮŠø÷Š”Ģā.
×÷·Ø£ŗ¢ŁŅŌµćBĪŖŌ²ŠÄ£¬ŹŹµ±³¤¶ČĪŖ°ė¾¶»»”£¬½»BAÓŚµćM£¬½»BCÓŚµćN.
¢Ś·Ö±šŅŌµćM£¬NĪŖŌ²ŠÄ”¢“óÓŚ![]() MNµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚµćO.
MNµÄ³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚµćO.
¢ŪĮ¬½ÓBO²¢ŃÓ³¤£¬½»ACÓŚµćD.
(1)Ēó”ĻABDµÄ¶ČŹż.
(2)Į½øöĻćĮĻ¼Ó¹¤³§(·Ö±šŹĒµćAŗĶµćC)ŗĶŅ»øö¾ÓĆńĒų(µćB)µÄĪ»ÖĆŹ¾ŅāĶ¼Ē”ŗĆŹĒ”÷ABC£¬Į½øöĻćĮĻ¼Ó¹¤³§ĻėŗĻ׏ŠŽ½ØŅ»øöĪŪĖ®“¦Ąķ³§(P)£¬ŗĆ½«Éś²śĖłµĆµÄĪŪĖ®“¦Ąķµ½ŗĻøńĖ®Ę½ŌŁÅÅ·Å.ĪŖĮĖ²»ĪŪČ¾¾ÓĆńµÄÉś»īÓĆĖ®£¬¼Ę»®øĆĪŪĖ®“¦Ąķ³§½ØÉčŌŚĻ߶ĪBDµÄŃÓ³¤ĻßÉĻ£¬²¢ĒŅøĆĪŪĖ®“¦Ąķ³§ÓėĮ½øöĻćĮĻ¼Ó¹¤³§µÄ¾ąĄėĻąµČ.ĒėÄćÅŠ¶ĻÄÜ·ńÕŅµ½Āś×ćÉĻŹöĢõ¼žµÄĪŪĖ®“¦Ąķ³§µÄĪ»ÖĆ£æ²¢ŌŚĶ¼ÖŠĄūÓĆ»Ķ¼ĖµĆ÷ĄķÓÉ.(±£Įō×÷Ķ¼ŗŪ¼££¬²»ŅŖĒóŠ“×÷·Ø)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
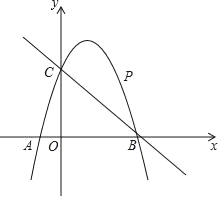
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹży=ax2+2x+cµÄĶ¼Ļó¾¹żµćC£Ø0£¬3£©£¬ÓėxÖį·Ö±š½»ÓŚµćA£¬µćB£Ø3£¬0£©£®µćPŹĒÖ±ĻßBCÉĻ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£®
£Ø1£©Ē󶞓ĪŗÆŹży=ax2+2x+cµÄ±ķ“ļŹ½£»
£Ø2£©Į¬½ÓPO£¬PC£¬²¢°Ń”÷POCŃŲyÖį·ÕŪ£¬µĆµ½ĖıߊĪPOP”äC£®ČōĖıߊĪPOP”äCĪŖĮāŠĪ£¬ĒėĒó³ö“ĖŹ±µćPµÄ×ų±ź£»
£Ø3£©µ±µćPŌĖ¶Æµ½Ź²Ć“Ī»ÖĆŹ±£¬ĖıߊĪACPBµÄĆ껿×ī“ó£æĒó³ö“ĖŹ±PµćµÄ×ų±źŗĶĖıߊĪACPBµÄ×ī“óĆ껿£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com