
【题目】(阅读理解)
用![]() 的矩形瓷砖,可拼得一些长度不同但宽度均为
的矩形瓷砖,可拼得一些长度不同但宽度均为![]() 的矩形图案.
的矩形图案.
已知长度为![]() 的所有图案如下:
的所有图案如下:

(尝试操作)
在所给方格中(假设图中最小方格的边长为![]() ),尝试画出所有用
),尝试画出所有用![]() 的“矩形瓷砖”拼得的“长度是
的“矩形瓷砖”拼得的“长度是![]() ,但宽度均为
,但宽度均为![]() ”的矩形图案示意图.
”的矩形图案示意图.

(归纳发现)
观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.

(规律概括)
描述一下你发现的规律: .
【答案】【尝试操作】:见解析;【归纳发现】5,8,13;【规律概括】:从长度30cm的图案开始,所有不同图案的个数是前面两个个数的和
【解析】
根据已知条件作图可知40cm时,所有图案个数5个;猜想得到结论.
解:(1)【尝试操作】
长度为40cm可以为:
①![]() ,可画出一种;②
,可画出一种;②![]() ,可画出一种;
,可画出一种;
③![]() ,可画出3种,分别是20cm的在左侧,右侧和中间.
,可画出3种,分别是20cm的在左侧,右侧和中间.
故如图:
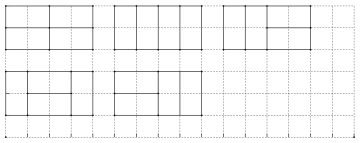
(2)【归纳发现】
根据作图可知40cm时,所有图案为5个;50cm时,所有图案个数8个;
60cm时,所有图案个数13个;
故答案为5,8,13;
(3)【规律概括】
中的数据寻找规律,可发现:
从长度30cm的图案开始,所有不同图案的个数是前面两个个数的和.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
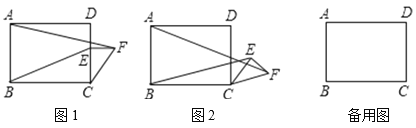
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线L:y=ax2+bx+c经过点A(-3,0)、B(0,4)和F(4,0).
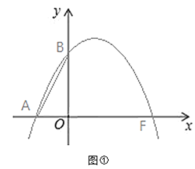
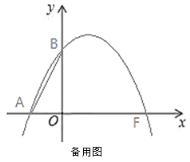
(1)求抛物线L的解析式;
(2)在图①抛物线L上,求作点C(保留作图痕迹,不写作法),使∠BAC=∠FAC,并求出点C的坐标;
(3)在图①中,若点D为抛物线上一动点,过点D作DH⊥x轴于点H,交直线AC于点G,过点C作CK⊥x轴于点K,连接DC,当以点G,C,D为顶点的三角形与△ACK相似时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为![]() 元,当销售单价定为
元,当销售单价定为![]() 元时,每天可以销售
元时,每天可以销售![]() 件.市场调查反映:销售单价每提高
件.市场调查反映:销售单价每提高![]() 元,日销量将会减少
元,日销量将会减少![]() 件,物价部门规定:销售单价不能超过
件,物价部门规定:销售单价不能超过![]() 元,设销售单价为
元,设销售单价为![]() (元).
(元).
(1)要使日销售利润为![]() 元,销售单价应定为多少元;
元,销售单价应定为多少元;
(2)求日销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)的函数关系式,当
(元)的函数关系式,当![]() 为何值时,日销售利润最大,并求出最大利润.
为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为12,E是边CD的中点,连接AE,折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“全民健身”时代的到来,健身已经成为推广文明生活的重要途径,成为国民增强身体素质和提高身体免疫力的重要方法.某校为促进学生对健身知识的了解,在七、八年级中开展了“健身知识知多少”的竞赛活动.现从该校七、八年级中各随机抽取![]() 名学生的竞赛成绩进行整理描述和分析,下面给出了部分信息:
名学生的竞赛成绩进行整理描述和分析,下面给出了部分信息:
a.七年级![]() 名学生成绩为:
名学生成绩为:
![]()
![]()
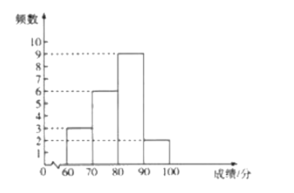
b.八年级![]() 名学生成绩的频数分布直方图如图:
名学生成绩的频数分布直方图如图:
c.八年级成绩在![]() 这一组的是:
这一组的是:
![]()
d.七、八年级成绩的平均数、中位数、众数如下:
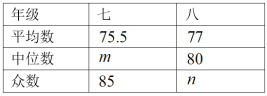
根据以上信息,回答下列问题:
(1)表中![]() , .
, .
(2)一名七年级学生和一名八年级学生发生了争论.均认为本年级的成绩更好.请你写出他们的理由:
七年级学生理由: ;
八年级学生理由: ;
(3)若该校七、八年级各有![]() 名学生.请估计该校七、八年级此次竞赛成绩优秀
名学生.请估计该校七、八年级此次竞赛成绩优秀![]() 的学生共有多少人.
的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为![]() 的中点.
的中点.
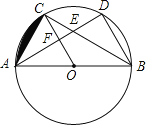
(1)求证:OF∥BD;
(2)若![]() ,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
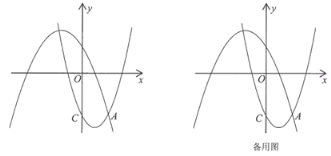
【题目】如图,在平面直角坐标系xOy中,抛物线L1:![]() 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2:![]() 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
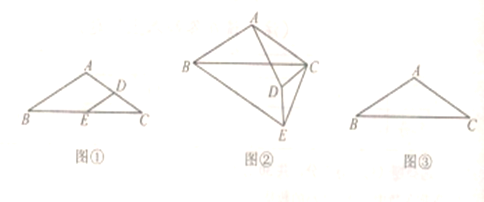
【题目】(1)探索发现
如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接,则
的中点,连接,则![]() 的值为 .
的值为 .
(2)拓展探索
若将![]() 绕点
绕点![]() 逆时针方向旋转一周,在旋转过程中
逆时针方向旋转一周,在旋转过程中![]() 的值有没有变化?以图②的情形给出证明.
的值有没有变化?以图②的情形给出证明.
(3)问题解决
如图③,当![]() 旋转到
旋转到![]() 三点在同一条直线上是,直接写出
三点在同一条直线上是,直接写出![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com