试题分析:(1)将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,易知点F′、B、E在一直线上.证得AF′E≌△AFE.从而得到EF=F′E=BE+DF;
(2)由(1)得EF=x+y再根据CF=1-y,EC=1-x,得到(1-y)
2+(1-x)
2=(x+y)
2.化简即可得到y=
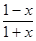
(0<x<1).
(3)当点E在点B、C之间时,由(1)知EF=BE+DF,故此时⊙E与⊙F外切;当点E在点C时,DF=0,⊙F不存在.当点E在BC延长线上时,将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,证得△AF′E≌△AFE.即可得到EF=EF′=BE-BF′=BE-FD.从而得到此时⊙E与⊙F内切.
(4)△EGF与△EFA能够相似,只要当∠EFG=∠EAF=45°即可.这时有 CF=CE.设BE=x,DF=y,由(3)有EF=x-y.由CE
2+CF
2=EF
2,得(x-1)
2+(1+y)
2=(x-y)
2.化简可得 y=
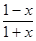
(x>1).又由 EC=FC,得x-1=1+y,即x-1=1+
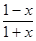
,化简得x
2-2x-1=0,解之即可求得BE的长
试题解析:
(1)猜想:EF=BE+DF.理由如下:
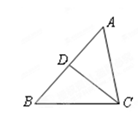
将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,易知点F′、B、E在一直线上.如图1.
∵AF′=AF,
∠F′AE=∠1+∠3=∠2+∠3=90°-45°=45°=∠EAF,
又AE=AE,
∴△AF′E≌△AFE.
∴EF=F′E=BE+DF;
(2)由(1)得EF=x+y
又CF=1-y,EC=1-x,
∴(1-y)
2+(1-x)
2=(x+y)
2.
化简可得y=
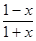
(0<x<1);
(3)①当点E在点B、C之间时,由(1)知EF=BE+DF,故此时⊙E与⊙F外切;
②当点E在点C时,DF=0,⊙F不存在.
③当点E在BC延长线上时,将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,图2.
有AF′=AF,∠1=∠2,BF′=FD,
∴∠F′AF=90°.
∴∠F′AE=∠EAF=45°.
又 AE=AE,
∴△AF′E≌△AFE.
∴EF=EF′=BE-BF′=BE-FD.
∴此时⊙E与⊙F内切.
综上所述,当点E在线段BC上时,⊙E与⊙F外切;当点E在BC延长线上时,⊙E与⊙F内切;
(4)△EGF与△EFA能够相似,只要当∠EFG=∠EAF=45°即可.
这时有CF=CE.
设BE=x,DF=y,由(3)有EF=x-y.
由CE
2+CF
2=EF
2,得(x-1)
2+(1+y)
2=(x-y)
2.
化简可得 y=
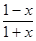
(x>1).
又由EC=FC,得x-1=1+y,即x-1=1+
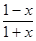
,化简得
x
2-2x-1=0,解之得
x=1+
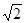
或x=1-
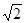
(不符题意,舍去).
∴所求BE的长为1+
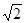
.



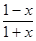 (0<x<1);(3)⊙E与⊙F外切;(4)BE的长为1+
(0<x<1);(3)⊙E与⊙F外切;(4)BE的长为1+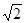 .
.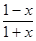
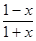 (x>1).又由 EC=FC,得x-1=1+y,即x-1=1+
(x>1).又由 EC=FC,得x-1=1+y,即x-1=1+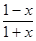 ,化简得x2-2x-1=0,解之即可求得BE的长
,化简得x2-2x-1=0,解之即可求得BE的长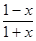 (0<x<1);
(0<x<1);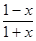 (x>1).
(x>1).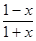 ,化简得
,化简得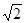 或x=1-
或x=1-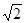 (不符题意,舍去).
(不符题意,舍去).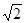 .
.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案




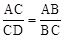 ; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )
; ④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的有( )