练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．一次函数y=kx+b与y=2x+1平行，且经过点（-3，4），求此函数的解析式．

    分析 先根据两直线平行，可以求得系数k的值，再根据直线经过已知的点，可以求得常数项b的值．

    解答 解：∵一次函数y=kx+b与y=2x+1平行，
    ∴k=2，
    又∵一次函数y=2x+b图象经过点（-3，4），
    ∴4=-6+b，
    解得b=10，
    ∴一次函数的解析式为：y=2x+10．

    点评 本题主要考查了两条直线平行的问题，若两条直线是平行的关系，那么他们的自变量系数相同，即直线y1=k1x+b1与直线y2=k2x+b2平行，那么k1=k2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．某市种植基地有A、B两个品种的树苗出售，已知A种比B种每株多2元，买1株A种树苗和2株B种树苗共需20元．
    （1）问A、B两种树苗每株分别是多少元？
    （Ⅱ）为扩大种植，某农户准备购买A、B两种树苗共360株，且A种树苗数量不少于B种数量的一半，问至少购买A种树苗多少株？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．体育委员统计了全班同学60秒跳绳的次数，并列出頻数分布表．
    次数60≤x＜8080≤x＜100100≤x＜120120≤x＜140140≤x＜160160≤x＜180
    頻数24211384
    （1）全班有多少学生？
    （2）组距是多少？组数是多少？
    （3）跳绳次数x在120≤x＜160范围的学生有多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．等腰三角形的周长是40cm，腰长y（cm）是底边长x（cm）的函数，此函数解析式和自变量取值范围正确的是（　　）
    A．y=-2x+40（0＜x＜20）B．y=-0.5x+20（10＜x＜20）
    C．y=-2x+40（10＜x＜20）D．y=-0.5x+20（0＜x＜20）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．对于某些数学问题，灵活运用整体思想，可以化难为易．在解二元一次方程组时，就可以运用整体代入法：如解方程组：$\left\{\begin{array}{l}x+2（x+y）=3---①\\ x+y=1---②\end{array}\right.$
    解：把②代入①得，x+2×1=3，解得x=1．
    把x=1代入②得，y=0．
    所以方程组的解为 $\left\{\begin{array}{l}x=1\\ y=0.\end{array}\right.$
    请用同样的方法解方程组：$\left\{\begin{array}{l}2x-y-2=0----①\\ \frac{2x-y+5}{7}+2y=9----②\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列调查中，最适宜采用全面调查方式的是（　　）
    A．对广水市中学生每天学习所用时间的调查
    B．对全国中学生心理健康现状的调查
    C．对某班学生进行6月5日是“世界环境日”知晓情况的调查
    D．对广水市初中学生视力情况的调查

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知y=（k-1）x|k|-k是一次函数．
    （1）求k的值；
    （2）若点（2，a）在这个一次函数的图象上，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知点P（1，m）、Q（n，1）在反比例函数y=$\frac{5}{x}$的图象上，直线y=kx+b经过点P、Q，且与x轴、y轴的交点分别为A、B两点．
    （1）求 k、b的值；
    （2）O为坐标原点，C在直线y=kx+b上且AB=AC，点D在坐标平面上，顺次联结点O、B、C、D的四边形OBCD满足：BC∥OD，BO=CD，求满足条件的D点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

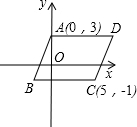    5．如图所示，在平面直角坐标系中，AD∥BC∥x轴，AD=BC=7，A（0，3），C（5，-1）．
    （1）求B、D两点坐标；
    （2）求四边形ABCD面积．

    查看答案和解析>>

    同步练习册答案