
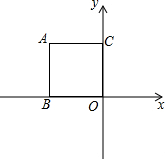
 如图,在平面直角坐标系中,已知A(-8,8),B(-8,0),C(0,8),连结AB,AC,若画出含边长为5的等腰三角形,A为顶角的顶点,另外两个顶点在折线AB-BO-OC-CA上,则等腰三角形的面积为$\frac{5}{2}$或20$\sqrt{2}$-$\frac{25}{4}$.
如图,在平面直角坐标系中,已知A(-8,8),B(-8,0),C(0,8),连结AB,AC,若画出含边长为5的等腰三角形,A为顶角的顶点,另外两个顶点在折线AB-BO-OC-CA上,则等腰三角形的面积为$\frac{5}{2}$或20$\sqrt{2}$-$\frac{25}{4}$. 分析 分两种情况:
①若5为腰,如图1,AE=AF=5,代入面积公式可求得等腰△AEF的面积;
②若5为底边,如图2,EF=5,分别求AO和OG,则AG=AO-OG=8$\sqrt{2}$-$\frac{5}{2}$,代入面积公式可求得等腰△AEF的面积.
解答 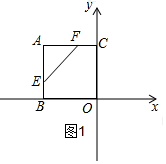 解:∵A(-8,8),B(-8,0),C(0,8),
解:∵A(-8,8),B(-8,0),C(0,8),
∴AB=BO=OC=AC=8,
∴四边形ABOC为菱形,
∵∠BOC=90°,
∴菱形ABOC为正方形,
分两种情况:
①若5为腰,如图1,AE=AF=5,
S△AEF=$\frac{1}{2}$AE•AF=$\frac{1}{2}$×5×5=$\frac{25}{2}$;
②若5为底边,如图2,EF=5,
连接AO,交EF于G,
∵AC=AB,AE=AF,∠ABO=∠ACO=90°,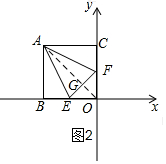
∴Rt△ABE≌△Rt△ACF(HL),
∴∠BAE=∠FAC,BE=CF,
∵OB=OC,
∴OE=OF,
∵四边形ABOC是正方形,
∴∠BAO=∠OAC=45°,
∴∠EAG=∠FAG,
∴AG⊥EF,EG=FG,
由勾股定理得:AO=$\sqrt{{8}^{2}+{8}^{2}}$=8$\sqrt{2}$,
OG=$\frac{1}{2}$EF=$\frac{5}{2}$,
∴AG=AO-OG=8$\sqrt{2}$-$\frac{5}{2}$,
S△AEF=$\frac{1}{2}$EF•AG=$\frac{1}{2}$×5×(8$\sqrt{2}$-$\frac{5}{2}$)=20$\sqrt{2}$-$\frac{25}{4}$;
则等腰三角形的面积为$\frac{5}{2}$或20$\sqrt{2}$-$\frac{25}{4}$.
点评 本题考查了等腰三角形的性质及坐标与图形的性质,明确等边对等角,熟练掌握等腰三角形三线合一的性质,本题采用了分类讨论的思想,根据图形及坐标表示线段的长,代入面积公式即可求其面积.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com