
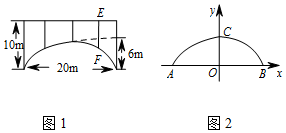
分析 (1)根据题目可知A,B,C的坐标,设出抛物线的解析式代入可求解.
(2)设F点的坐标为(5,yF)可求出支柱MN的长度.
(3)根据题意得到三辆汽车最右边到原点的距离为1+3×2=7,当x=7时,得到y=-$\frac{3}{50}$×49+6=3.06>3,于是得到结论.
解答 解:(1)根据题目条件A,B,C的坐标分别是(-10,0),(10,0),(0,6),
设抛物线的解析式为y=ax2+c,
将B,C的坐标代入y=ax2+c,
得$\left\{\begin{array}{l}{6=c}\\{0=100a+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{3}{50}}\\{c=6}\end{array}\right.$.
所以抛物线的表达式y=-$\frac{3}{50}$x2+6;
(2)可设F(5,yF),于是yF=-$\frac{3}{50}$×52+6=4.5,
从而支柱EF的长度是10-4.5=5.5米;
(3)根据题意,三辆汽车最右边到原点的距离为:1+3×2=7,
当x=7时,y=-$\frac{3}{50}$×49+6=3.06>3,
故可以并排行驶宽2m,高3m的三辆汽车.
点评 本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,五边形ABCDE为⊙O的内接五边形,$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,$\widehat{AE}$=$\widehat{ED}$,BD、BE分别与AC交于点F、G,AD与BE交于点H.
如图,五边形ABCDE为⊙O的内接五边形,$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,$\widehat{AE}$=$\widehat{ED}$,BD、BE分别与AC交于点F、G,AD与BE交于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com