
如图已知四边形ABCD是平行四边形,AC与BD相交于O点,且BC⊥AC,AB=8,∠ABC=30°,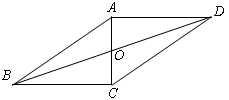
(1)求AD和BD的长;
(2)求平行四边形ABCD的面积.
(1)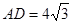 ,
,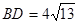 ;(2)
;(2)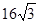
解析试题分析:(1)先根据含30°的直角三角形的性质求得AC的长,再在Rt△ABC中根据勾股定理求得BC的长,再根据平行四边形的性质求得AD、OD、AO的长,最后根据勾股定理求解即可;
(2)根据平行四边形的面积公式求解即可.
(1)∵BC⊥AC,AB=8,∠ABC=30°,
∴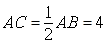
在Rt△ABC中,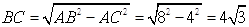
∵四边形ABCD是平行四边形,
∴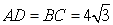
∵AC与BD相交于O点,
∴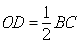 ,
,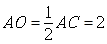
在Rt△AOD中,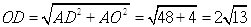
∴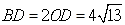 ;
;
(2)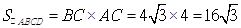 .
.
考点:含30°的直角三角形的性质,平行四边形的性质,各个定理
点评:平行四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
如图,在四边形ABCD中,AB=BC,对角线BD平分ÐABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。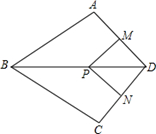
(1)求证:ÐADB=ÐCDB;
(2)若ÐADC=90°,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.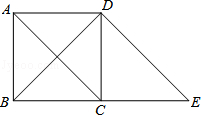
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在正方形铁皮上剪下一个圆和扇形(圆与扇形外切,且与正方形的边相切),
使之恰好围成如图所示的一个圆锥模型,设圆半径为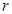 ,扇形半径为R,则R与
,扇形半径为R,则R与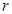 的关系是 ( )
的关系是 ( )
| A.R=2r | B.R="4r" |
| C.R=2πr | D.R=4πr |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com