
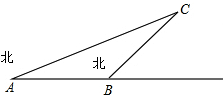
 一船在A处测得小岛C在北偏东75°的方向,船在A处向正东航行30海里到B处,再测C在它的东北方向上,求原出发点A与C的距离.
一船在A处测得小岛C在北偏东75°的方向,船在A处向正东航行30海里到B处,再测C在它的东北方向上,求原出发点A与C的距离. 分析 作BD⊥CA于D,在AD上取点E,使EA=EB,根据题意求出∠DEB的度数,设BD=x,表示出BE,AE,DE,根据勾股定理列出方程,求出x的值即可.
解答 解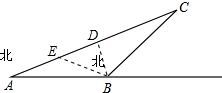 :作BD⊥CA于D,在AD上取点E,使EA=EB,
:作BD⊥CA于D,在AD上取点E,使EA=EB,
由题意得,∠A=15°,∠ABC=135°,
∴∠C=30°,
∵EA=EB,
∴∠EBA=∠A=15°,
∴∠DEB=30°,
设BD=x,则BE=2x,AE=2x,
由勾股定理得,DE=$\sqrt{3}$x,又AB=30,
∴x2+(2x+$\sqrt{3}$x)2=900,
解得,x=15$\sqrt{2-\sqrt{3}}$,
则AC=2x+2$\sqrt{3}$x=30$\sqrt{2-\sqrt{3}}$+30$\sqrt{3\sqrt{3}-3}$.
答:点A与C的距离为30$\sqrt{2-\sqrt{3}}$+30$\sqrt{3\sqrt{3}-3}$.
点评 本题考查的是解直角三角形的应用,正确作出辅助线、灵活运用锐角三角函数的概念和勾股定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com