

���� ��1��ֱ�Ӹ���ͼ��д����ʽ��
��2��������ʽ���루1���Ľ��۶Աȣ��ó����ε�ʽ�ӣ�������ֵ���ɣ�
��3���ٻ���ͼ�Σ��𰸲�Ψһ��
�ڸ���ԭͼ�����=��Ϻ��ε�����ó���ʽ��
��� ��1����a+b+c��2=a2+b2+c2+2ab+2ac+2bc��
�ʴ�Ϊ����a+b+c��2=a2+b2+c2+2ab+2ac+2bc��
��2��a2+b2+c2=��a+b+c��2-2ab-2ac-2bc��
=112-2��38��
=45��
��3������ͼ��ʾ��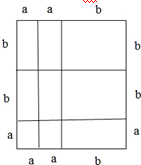
������ͼ��ʾ�ľ������=��2a+b����a+2b����
������2���߳�Ϊa�������Ρ�5���߳��ֱ�Ϊa��b�ij����Ρ�2���߳�Ϊb��С��������ɣ��������Ϊ2a2+5ab+2b2��
��2a2+5ab+2b2=��2a+b����a+2b����
�ʴ�Ϊ��2a2+5ab+2b2=��2a+b����a+2b����
���� ������һ���Ķ��������⣬��������ȫƽ��ʽ�ļ��α������⼰��ʽ�ֽ��Ӧ�ã��뼸��ͼ�����ϣ�ͨ�������ֱ�����⡢�����ȫƽ����ʽ���Ƶ����̣�ͨ������ͼ��֮���������ϵ����ȫƽ����ʽ�������ν��ͣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15�� | B�� | 25�� | C�� | 35�� | D�� | 55�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ���Ҷ��� | B�� | ���Ҷ����� | C�� | �ԣ��Ҳ��� | D�� | �ײ��ԣ��Ѷ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com