
【题目】如图,AB为⊙O的直径,PQ切⊙O于E,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=2,EC=![]() ,∠BAC=60°,求⊙O的半径.
,∠BAC=60°,求⊙O的半径.
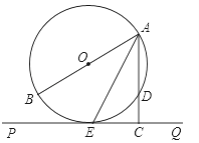
【答案】(1)证明见解析;(2)2.
【解析】
试题(1)连接OE,根据切线的性质就可以得出OE⊥PQ,就可以得出OE∥AC,可以得出∠BAE=∠CAE而得出结论;
(2)连接BE,由AE平分∠BAC就可以得出∠BAE=∠CAE=30°,就可以求出AE=2![]() ,在Rt△ABE中由勾股定理可以求出AB的值,从而求出结论.
,在Rt△ABE中由勾股定理可以求出AB的值,从而求出结论.
试题解析:(1)证明:连接OE,
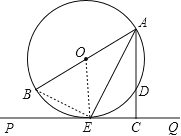
∴OA=OE,
∴∠OEA=∠OAE.
∵PQ切⊙O于E,
∴OE⊥PQ.
∵AC⊥PQ,
∴OE∥AC.
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,
∴AE平分∠BAC.
(2)解:连接BE,
∵AB是直径,
∴∠AEB=90°.
∵∠BAC=60°,
∴∠OAE=∠EAC=30°.
∴AB=2BE.
∵AC⊥PQ,
∴∠ACE=90°,
∴AE=2CE.
∵CE=![]() ,
,
∴AE=2![]() .
.
设BE=x,则AB=2x,由勾股定理,得
x2+12=4x2,
解得:x=2.
∴AB=4,
∴⊙O的半径为2.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
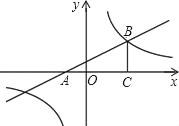
【题目】如图,平面直角坐标系中,直线y=![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 在第一象限内交于点B,BC⊥x轴于点C,OC=3AO.
在第一象限内交于点B,BC⊥x轴于点C,OC=3AO.
(1)求双曲线的解析式;
(2)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
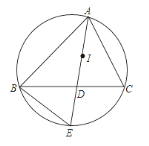
【题目】如图,I是△ABC的内心,AI的延长线交边BC于点D,交△ABC的外接圆于点E.
(1)BE与IE相等吗?请说明理由.
(2)连接BI,CI,CE,若∠BED=∠CED=60°,猜想四边形BECI是何种特殊四边形,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
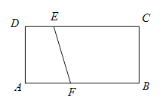
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
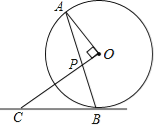
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
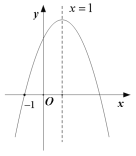
【题目】抛物线![]() 的图象如图所示,抛物线过点
的图象如图所示,抛物线过点![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为一切实数);⑤
为一切实数);⑤![]() ;正确的个数有( ).
;正确的个数有( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
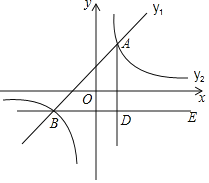
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里有 ![]() 个除颜色外都相同的球,其中有
个除颜色外都相同的球,其中有 ![]() 个红球,
个红球, ![]() 个黄球.
个黄球.
(1) 若从中随意摸出一个球,求摸出红球的可能性;
(2) 若要使从中随意摸出一个球是红球的可能性为 ![]() ,求袋子中需再加入几个红球?
,求袋子中需再加入几个红球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com