

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 2 |
 度是每分钟3个单位长度,直线PM交BC于点Q,当直线PM与正方形OABC没有公共点的时候,动点P就停止运动.
度是每分钟3个单位长度,直线PM交BC于点Q,当直线PM与正方形OABC没有公共点的时候,动点P就停止运动.| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 格不变,而制版费900元按六折收费,且甲乙两厂都规定一次印刷数量至少是500份.
格不变,而制版费900元按六折收费,且甲乙两厂都规定一次印刷数量至少是500份.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
 重叠部分的面积为S.
重叠部分的面积为S.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
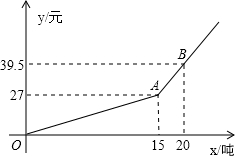 )与用水量x(吨)的函数关系如图所示.
)与用水量x(吨)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 4 |
 C,点D是直线AC上的一个动点.
C,点D是直线AC上的一个动点.| BE |
| CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com