
����Ŀ����ͼ��������A��B�����Ӧ���������ֱ�Ϊ20��30����P�͵�Q�ֱ�ͬʱ�ӵ�A�͵�O��������ÿ��2����λ���ȣ�ÿ��4����λ���ȵ��ٶ��������������˶������˶�ʱ��Ϊt�룮 ![]()
��1����t=2ʱ����P��Q�����Ӧ���������ֱ�����PQ=��
��2����C�������ϵ�B���һ�㣬���Ӧ������x����CB=2CA����x��ֵ��
��3���ڵ�P�͵�Q������ͬʱ����R��ÿ��8����λ���ȵ��ٶȴӵ�B��������ʼ�����˶���������Q���������������˶���������P���������������˶������Q���������������أ����������ֱ��P��Q��������ʱ����Rֹͣ�˶������R�˶���·��һ���Ƕ��ٸ���λ���ȣ���Rֹͣ��λ������Ӧ�����Ƕ��٣�
���𰸡�
��1��24��8��16
��2���⣺��CB=2CA��
��30��x=2��x��20����30��x=2��20��x����
��x= ![]() ��10
��10
��3���⣺��t���P��Q����������4t��2t=20��
��t=10��
��R�˶���·��һ����8��10=80����ʱP��Q��R��ͬһ�㣬���Ե�R��λ������Ӧ������40
���������⣺��1��t=2ʱ��OQ=2��4=8��PA=2��2=4��OP=24�� ��P��Q�ֱ��ʾ24��8��PQ=24��8=16��
���Դ���24��8��16��
�����㾫����������Ҫ����������ʹ���ʽ��ֵ�����֪ʶ�㣬��Ҫ���������ǹ涨��ԭ�㡢������λ���ȵ�һ��ֱ�ߣ������ʽ��ֵ��һ�����Ƚ�����ʽ����Ȼ���ٽ���ĸ��ȡֵ���룻�����ʽ��ֵ����ʱ������ĸ��ֵ����Ҫ���ü��ɣ������塱���������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.��2x2y3xy2=��6x2y2
B.����x��2y����x+2y��=x2��4y2
C.6x3y2��2x2y=3xy
D.��4x3y2��2=16x9y4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
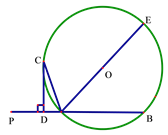
����Ŀ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD
��1����֤��CDΪ��O������
��2����DC+DA=6����O��ֱ��Ϊ10����AB�ij��ȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨һ�������� a��b=a��b��a+b+1���磬3��4=3��4��3+4+1=12��3+4+1=14����2��5= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ����װ�������ֱ��������1��2��3��С�����ǵ���״����С���ʵص���ȫ��ͬ��С���ȴӺ��������ȡ��һ��С��������Ϊx���Ž�����ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy��
(1)������״ͼ���б�������д��(x��y�����п��ܳ��ֵĽ����
(2)��С����С����ȡһ��С����ȷ���ĵ�(x��y�����ڷ���������![]() ͼ���ϵĸ��ʣ�
ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=90�㣬AB=AC��AD��BC��D��AEƽ�֡�BAD����BC��E���ڡ�ABC����һ��F��ʹFA��AE��FC��BC��
��1����֤��BE=CF��
��2����AB��ȡһ��M��ʹ��BM=2DE������ME
����֤��ME��BC��
�����EMC�Ķ�����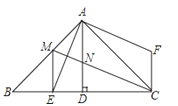
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����[a]��ʾ������a��������������磺[2.3]=2��[��4 ![]() ]=��5��[5]=5��
]=��5��[5]=5��
��1����[2 ![]() ]+[��3.6]��[��7]��ֵ��
]+[��3.6]��[��7]��ֵ��
��2����[a]=a��[a]����{2 ![]() }��[��2.4]+{��6
}��[��2.4]+{��6 ![]() }��
}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
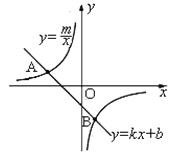
����Ŀ������ͼ����֪A��-4��2����B��n��-4����һ�κ���y=kx+b��ͼ��ͷ���������![]() ��ͼ����������㣮
��ͼ����������㣮
��1����m��n��ֵ��
��2����һ�κ����Ĺ�ϵʽ����
��3�����ͼ��ֱ��д��һ�κ���С�ڷ�����������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
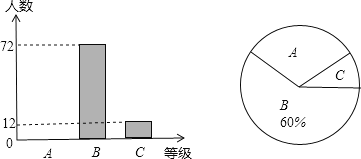
����Ŀ������ij��ѧΪ�˽�ѧ�������ʽ���״���������ȡ������ѧ�����в��ԣ����Խ����ΪA�����á�B���ϸ�C�����ϸ������ȼ��������ݲ��Խ�����Ƴ����������в�������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺
��1���˴ε��鹲��ȡ�������ˣ�����ͳ��ͼ��C����Բ�ĽǵĶ���Ϊ������
��2����ȫ����ͳ��ͼ��
��3������У����1800��ѧ������������ʽ���״��Ϊ���ϸ�ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com