
| A. | 16 | B. | 32 | C. | -16 | D. | -32 |
分析 首先求出$\frac{1}{a}$的值,进而得出${a^2}+\frac{1}{a^2}+2$=(a+$\frac{1}{a}$)2,代入求出即可.
解答 解:∵$a=\sqrt{7}-2\sqrt{2}$,
∴$\frac{1}{a}$=$\frac{1}{\sqrt{7}-2\sqrt{2}}$=$\frac{\sqrt{7}+2\sqrt{2}}{(\sqrt{7}-2\sqrt{2})(\sqrt{7}+2\sqrt{2})}$=-$\sqrt{7}$-2$\sqrt{2}$,
∴${a^2}+\frac{1}{a^2}+2$=(a+$\frac{1}{a}$)2=($\sqrt{7}$-2$\sqrt{2}$-$\sqrt{7}$-2$\sqrt{2}$)2=(-4$\sqrt{2}$)2=32.
故选:B.
点评 此题主要考查了二次根式的化简求值,得出$\frac{1}{a}$的值是解题关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
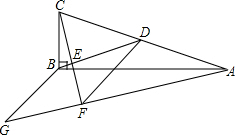 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
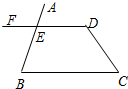 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它是三次三项式 | B. | 它是四次两项式 | ||
| C. | 它的最高次项是-6x2yz | D. | 它的常数项是1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
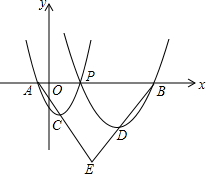 如图,已知点A(-1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于( )
如图,已知点A(-1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
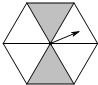 如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com