
【题目】请在网格坐标系中画出二次函数![]() 的大致图象(注:图中小正方形网格的边长为
的大致图象(注:图中小正方形网格的边长为![]() ),根据图象填空:
),根据图象填空:
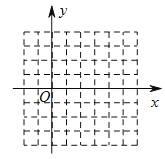
(![]() )当
)当![]() __________时,
__________时,![]() 有最__________值
有最__________值![]() __________.
__________.
(![]() )
)![]() 随
随![]() 的增大而减小的自变量
的增大而减小的自变量![]() 的取值范围是__________.
的取值范围是__________.
(![]() )结合图象直接写出
)结合图象直接写出![]() 时
时![]() 的范围:__________.
的范围:__________.
(![]() )结合图象直接写出
)结合图象直接写出![]() 时
时![]() 的取值范围:__________.
的取值范围:__________.
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知点A(a,3),点C(5,c),点B的纵坐标为6且横纵坐标互为相反数,直线AC![]() 轴,直线CB
轴,直线CB![]() 轴:
轴:
(1)写出A、B、C三点坐标;
(2)求△ABC的面积;
(3)若P为线段OB上动点且点P的横、纵坐标互为相反数,当△BCP的面积大于12小于16时,求点P横坐标取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.

解:∵AB∥CD(已知)
∴∠EFD=∠AEF( )
∵∠AEF=68°(已知)
∴∠EFD=∠AEF=68°( )
∵FG平分∠EFD(已知)
所以∠EFG=∠GFD=![]() ∠EFD=34°( )
∠EFD=34°( )
又因为KF⊥FG( )
所以∠KFG=90°( )
所以∠KFC=180°-∠GFD-∠KFG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1,可以得到![]() 这个等式,请解答下列问题:
这个等式,请解答下列问题:

(1)写出图2中所表示的数学等式______________;(最后结果)
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2的值;
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出一个面积为(5a+2b)(3a+5b)的长方形,求x+y+z的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠3=∠E.则AD与BE平行吗?
完成下面的解答过程(填写理由或数学式).
解:∵∠1=∠2(已知),
∴ ∥ (内错角相等,两直线平行),
∴∠E=∠ (两直线平行,内错角相等),
又∵∠E=∠3(已知),
∴∠3=∠ (等量代换),
∴AD∥BE( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=15cm,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立即改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
(1)若点P点Q同时出发,且当点P与点Q重合时,求t的值.
(2)若点P点Q同时出发,在P与Q相遇前,若点P是线段AQ的三等分点时,求t的值.
(3)若点P点Q同时出发,Q点与P点相遇后仍然继续往A点的方向运动到A点后再返回,求整个运动过程中PQ为6cm时t的值 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
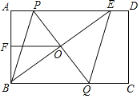
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系,并说明理由;
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国际无烟日”来临之际,小敏同学就一批公众对在餐厅吸烟所持的三种态度(彻底禁烟、建立吸烟室、其他)进行了调查,并把调查结果绘制成如图所示统计图,请根据图中的信息回答下列问题:

(1)被调查者中,不吸烟者中赞成“彻底禁烟”的人数有______人;
(2)本次抽样调查的样本容量为_______;
(3)被调查中,希望建立吸烟室的人数有______;
(4)某市现有人口约30万人,根据图中的信息估计赞成在餐厅彻底禁烟的人数约有______万人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】O为直线AB上的一点,OC⊥OD,射线OE平分∠AOD.

(1)如图①,判断∠COE和∠BOD之间的数量关系,并说明理由;
(2)若将∠COD绕点O旋转至图②的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com