
| A. | b≥-6 | B. | b≤4 | C. | -6≤b≤-4 | D. | 4≤b≤6 |
分析 先解不等式2x-b>-4时,得x>$\frac{b-4}{2}$;再求出函数y=2x-b沿x轴翻折后的解析式为y=-2x+b,解不等式-2x+b>-4,得x<$\frac{b+4}{2}$;根据x满足0<x<5,得出$\frac{b-4}{2}$=0,$\frac{b+4}{2}$=5,进而求出b的取值范围.
解答 解:∵y=2x-b,
∴当y>-4时,2x-b>-4,解得x>$\frac{b-4}{2}$;
∵函数y=2x-b沿x轴翻折后的解析式为-y=2x-b,即y=-2x+b,
∴当y>-4时,-2x+b>-4,解得x<$\frac{b+4}{2}$;
∴$\frac{b-4}{2}$<x<$\frac{b+4}{2}$,
∵x满足0<x<5,
∴$\frac{b-4}{2}$=0,$\frac{b+4}{2}$=5,
∴b=4,b=6,
∴b的取值范围为4≤b≤6.
故选D.
点评 本题考查了一次函数图象与几何变换,求出函数y=2x-b沿x轴翻折后的解析式是解题的关键.


科目:初中数学 来源: 题型:选择题
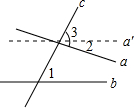 如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( )
如图,直线a,b被直线c所截,∠1=62°,∠3=80°,现逆时针转动直线a至a′位置,使a′∥b,则∠2的度数是( )| A. | 8° | B. | 10° | C. | 18° | D. | 28° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1,则$\widehat{AB}$的长为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
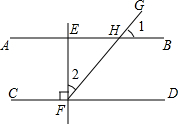 如图,直线AB∥CD,EF⊥CD,垂足为F,交AB于点E,射线FG交AB于点H.若∠1=30°,则∠2的度数为( )
如图,直线AB∥CD,EF⊥CD,垂足为F,交AB于点E,射线FG交AB于点H.若∠1=30°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
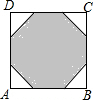 如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是8+8$\sqrt{2}$.
如图,在边长为2的正八边形中,把其不相邻的四条边均向两边延长相交成一个四边形ABCD,则四边形ABCD的周长是8+8$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com