
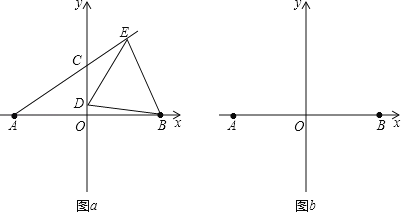
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 是
是![]() 轴上两点,其中
轴上两点,其中![]() ,点
,点![]() 都在
都在![]() 轴上,
轴上,![]() 在射线
在射线![]() 上(不与点
上(不与点![]() 重合),
重合),![]() ,连结
,连结![]() .
.
(1)求![]() 、
、![]() 的坐标;
的坐标;
(2)如图![]() ,若
,若![]() 在
在![]() 轴正半轴,
轴正半轴,![]() 在线段
在线段![]() 上,当
上,当![]() 时,求证:
时,求证:![]() 为等边三角形;(提示:连结
为等边三角形;(提示:连结![]() )
)
(3)当![]() 时,在图
时,在图![]() 中画出示意图,设
中画出示意图,设![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1) A(﹣4,0),B(4,0);(2)见解析;(3) 10或6
【解析】
(1)由a2+2ab+b2+|b-4|=0,得出(a+b)2+|b-4|=0,再根据非负数的性质,得出a=-4,b=4,即可得到A(-4,0),B(4,0);
(2)连接AD并延长至F,根据等腰三角形的性质以及三角形外角性质,即可得出∠BDF=∠DAO+∠DBO=2∠DAO,∠EDF=2∠DAE,进而得到∠EDB=60°,再根据DE=DB,即可得出△BDE为等边三角形;
(3)分两种情况进行讨论:①当C在y轴正半轴时,②当C在y轴负半轴时,分别判定全等三角形,根据全等三角形的对应边相等,分别求得n-m=4,m+n=-4,再根据mn=2,求得![]() 的值即可.
的值即可.
解:(1)∵a2+2ab+b2+|b﹣4|=0,∴(a+b)2+|b﹣4|=0,
又∵(a+b)2≥0,|b﹣4|≥0,∴(a+b)2=0,|b﹣4|=0,
∴a=﹣4,b=4,∴A(﹣4,0),B(4,0);
(2)证明:如图a,连接AD并延长至F,
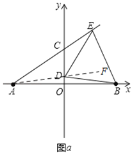
∵A(﹣4,0),B(4,0),∴OA=OB,∵OD⊥AB,∴DA=DB,
∴∠DAO=∠DBO,∴∠BDF=∠DAO+∠DBO=2∠DAO,∵DA=DB,DE=DB,
∴DA=DE,同理可得∠EDF=2∠DAE,
∴∠BDF+∠EDF=2∠DAE+2∠DAO=2∠CAO=60°,即∠EDB=60°,
又∵DE=DB,∴△BDE为等边三角形;
(3)分两种情况:
①当C在y轴正半轴时,如图b所示,过点E作EG⊥y轴于点G,
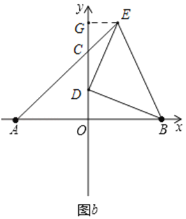
则∠GED+∠GDE=90°,∵DE⊥DB,∴∠ODB+∠GDE=90°,∴∠GED=∠ODB,
又∵∠DGE=∠DOB=90°,DE=DB,
∴在△DGE和△BOD中,
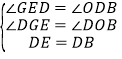 ,
,
∴△DGE≌△BOD(AAS)
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=m,OG=n,
由OG﹣OD=DG,得n﹣m=4,
∵mn=2,
∴![]() =10;
=10;
②当C在y轴负半轴时,如图c所示,过点E作EG⊥y轴于点G,
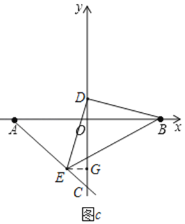
同理可得,△DGE≌△BOD,
∴OD=EG,DG=OB=4,
∵E(m,n),
∴OD=EG=﹣m,OG=﹣n,
由OD+OG=DG,得﹣m+(﹣n)=4,则m+n=﹣4,
∵mn=2,
∴![]() =6,
=6,
综上所述,![]() 的值为10或6.
的值为10或6.


科目:初中数学 来源: 题型:
【题目】如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知第三象限的点P(x,y)满足![]() ,
,![]() .
.
(1)求点P的坐标;
(2)①点P到x轴的距离为_______;
②把点P向右平移m个单位后得到P1,则点P1到x轴的距离为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校有一块长为(3a+b)m,宽为(2a+b)m的长方形空地,中间是边长(a+b)m的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
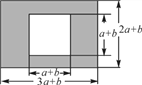
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为![]() 的正方形图形分割成四部分,观察图形,解答下列问题:
的正方形图形分割成四部分,观察图形,解答下列问题:
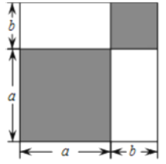
(1)根据图中条件,请用两种方法表示该阴影图形的总面积
方法1:_________________方法2__________________;
由此可得等量关系:______________________________;
应用该等量关系解决下列问题:
(2)若图中的a,b(![]() )满足
)满足![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com