
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.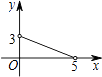
C.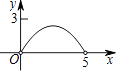
D.
【答案】C
【解析】解:由翻折的性质得,∠CPD=∠C′PD,
∵PE平分∠BPC1 ,
∴∠BPE=∠C′PE,
∴∠BPE+∠CPD=90°,
∵∠C=90°,
∴∠CPD+∠PDC=90°,
∴∠BPE=∠PDC,
又∵∠B=∠C=90°,
∴△PCD∽△EBP,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴y= ![]() x(5﹣x)=﹣
x(5﹣x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴函数图象为C选项图象.
故选:C.
根据翻折变换的性质可得∠CPD=∠C′PD,根据角平分线的定义可得∠BPE=∠C′PE,然后求出∠BPE+∠CPD=90°,再根据直角三角形两锐角互余求出∠CPD+∠PDC=90°,从而得到∠BPE=∠PDC,根据两组角对应相等的三角形相似求出△PCD和△EBP相似,根据相似三角形对应边成比例列式求出y与x的关系式,再根据二次函数的图象解答即可.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】小明解方程![]() -
-![]() =1的过程如下:
=1的过程如下:
解:方程两边乘x,得1-(x-2)=1.①
去括号,得1-x-2=1.②
移项,得-x=1-1+2.③
合并同类项,得-x=2.④
解得x=-2.⑤
所以,原分式方程的解为x=-2.⑥
请指出他解答过程中的错误,并写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.
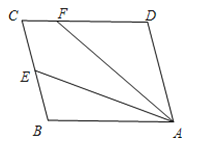
(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;
(2)求证:AF=CD+CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() -
-![]() =1的过程如下:
=1的过程如下:
解:方程两边乘x,得1-(x-2)=1.①
去括号,得1-x-2=1.②
移项,得-x=1-1+2.③
合并同类项,得-x=2.④
解得x=-2.⑤
所以,原分式方程的解为x=-2.⑥
请指出他解答过程中的错误,并写出正确的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com