
【题目】如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
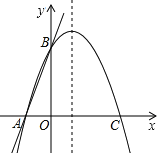
(1)求A、B的坐标;
(2)求抛物线的解析式;
(3)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
【答案】(1)A(﹣1,0),B(0,3);(2)y=﹣x2+2x+3;(3)存在,Q(1,1),(1,0),(1,![]() ),(1,﹣
),(1,﹣![]() ).
).
【解析】
(1)已知一次函数解析式,分别令![]() 即可解决.
即可解决.
(2)设出抛物线的一般式,将![]() 三点坐标代入用待定系数法即可解决.
三点坐标代入用待定系数法即可解决.
(3)抛物线解析式后可得其对称轴为![]() ,可设
,可设![]() ,此时需要分三种情况讨论:
,此时需要分三种情况讨论:![]() ,每一种的线段长度用
,每一种的线段长度用![]() 表示出来,列方程求解即可.
表示出来,列方程求解即可.
解:(1)∵y=3x+3,
∴当x=0时,y=3,
当y=0时,x=﹣1,
∴A(﹣1,0),B(0,3).
(2)设抛物线的解析式为![]() ,由题意,得
,由题意,得
 ,
,
解得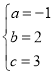
∴抛物线的解析式为:y=﹣x2+2x+3.
(3)∵y=﹣x2+2x+3,
∴y=﹣(x﹣1)2+4
∴抛物线的对称轴为x=1,设![]() ,
,
(1)当AQ=BQ时,如图,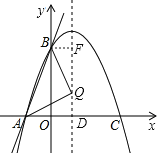
由勾股定理可得
BQ=![]() ,
,
AQ=![]()
AQ=BQ
即![]() ,
,
解得![]() ,
,
∴Q(1,1);
(2)如图: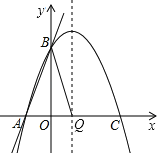
当AB是腰时,Q是对称轴与x轴交点时,AB=BQ,
∴![]()
解得:![]() 或6,
或6,
当Q点的坐标为(1,6)时,其在直线AB上,A、B和Q三点共线,舍去,
则此时Q的坐标是(1,0);
(3)当AQ=AB时,如图:
![]() ,
,
解得![]() ,
,
则Q的坐标是(1,![]() )和(1,﹣
)和(1,﹣![]() ).
).
综上所述:Q(1,1),(1,0),(1,![]() ),(1,﹣
),(1,﹣![]() ).
).


科目:初中数学 来源: 题型:
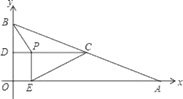
【题目】在平面直角坐标系中,已知点A、B的坐标分别为(10,0)、(0,4),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C以每秒1个单位匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P运动的时间为_____秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
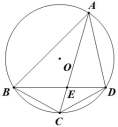
【题目】已知:如图,四边形 ABCD 内接于⊙ O ,AC 和 BD 相交于E , BC = CD = 4 , AE = 6 ,且 BE 和 DE 的长是正整数,求 BD 的 长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以用![]() 表示
表示![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示
,可表示![]() ,
,![]() ,
,![]() .
.
(1)已知二次函数![]() ;
;
①求证:不论![]() 为何值,此函数图像与
为何值,此函数图像与![]() 轴总有两个交点;
轴总有两个交点;
②若![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)已知函数![]() ,
,![]() ,若实数
,若实数![]() 、
、![]() 使得
使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
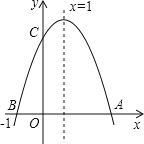
【题目】如图,二次函数y=ax2+bx+c(b≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3 ②a+b+c<0 ③ac>0 ④当y>0时,﹣1<x<3,其中正确的结论是( )
A.②④B.①③C.①④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
(1)若S1+S3=4S2 ,求Q点坐标;
(2)连结AQ,求AP+AQ的最小值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
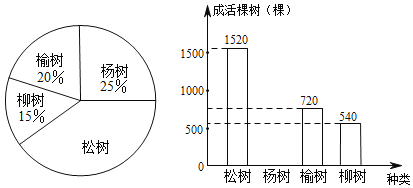
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该市今年共种树16万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桑桑同学利用寒假30天的时间贩卖草莓,某品种草莓的成本为10元/千克,该品种草莓在第![]() 天的销售量与销售单价如下表:
天的销售量与销售单价如下表:
销售量 |
|
销售单价 | 当 |
当 |
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com