
 ①当
①当![]() ;
;
当![]() ;
;
当![]() ;
;
当![]() ;
;
②当![]() ;当
;当![]() ;
;
当![]() ;当
;当![]() 。
。
根据以上结论,解答下列问题:
(1)猜想当![]() 和
和![]() 时,分别能得到什么结论(其中m、n均为正整数)?
时,分别能得到什么结论(其中m、n均为正整数)?
(2)进一步猜想当![]() 时,有何结论(其中m、n均为正整数)?并证明你的结论;
时,有何结论(其中m、n均为正整数)?并证明你的结论;
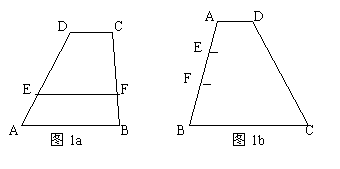
(3)如图1b,有一块梯形耕地ABCD,AD∥BC,AD=100米,BC=300米,AB=500米,在AB上取两点E、F,使AE=200米,EF=150米,分别从E、F两处为起点开挖两条平行于两底的水渠,直到另一腰,求这两条水渠的总长度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com