
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论正确的有__________.(填序号)

【答案】①②③
【解析】
结合已知条件,利用AAS即可判定△ABE≌△ACF,可知①正确;由①可得AE=AF,AC=AB,即可求得BF=CE,再利用AAS判定△BDF≌△CDE,可知②正确;由②可得DE=DF,根据角平分线的判定定理可得点D在∠BAC的平分线上,可知③正确;不能够判定④正确.
∵BE⊥AC于E,CF⊥AB于F,
∴∠AFC=∠AEB=90°,
在△ABE和△ACF中,
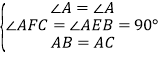 ,
,
∴△ABE≌△ACF(AAS),
故①选项正确,
由①得AE=AF,AC=AB,
∴BF=CE,
在△BDF和△CDE中,
 ,
,
∴△BDF≌△CDE,选项②正确,
由②得,DE=DF,
∵CF⊥AB于F,BE⊥AC于E,
∴点D在∠BAC的平分线上,选项③正确,
而点F不一定是AB的中点,故④错误.
综上,正确的结论为:①②③.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表所 示是该市居民“一户一表”生活用水及提示计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/ 吨 | 单价:元/ 吨 |
17 吨以下 | a | 0.80 |
超过 17 吨但不超过 30 吨的部分 | b | 0.80 |
超过 30 吨的部分 | 6.00 | 0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费自来水费用 污水处理费用)
已知小明家 2017 年 5 月份用水 20 吨,交水费 66 元;6 月份用水 25 吨交水费91元;
(1)求a 、b 的值;
(2)为了节约开支,小明家计划把 7 月份的水费控制在不超过家庭月收入的2% .若小明家的月收入为 9200 元,则小明家 7 月份最多能用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足![]() .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 平面内,没有公共点的两条线段平行
B. 平面内,没有公共点的两条射线平行
C. 没有公共点的两条直线互相平行
D. 互相平行的两条直线没有公共点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( ) 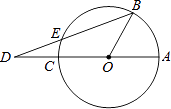
A.DE=EB
B.![]() DE=EB
DE=EB
C.![]() DE=DO
DE=DO
D.DE=OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y= ![]() (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( ) 
A.减小
B.增大
C.先减小后增大
D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校改造一个边长为![]() 米的正方形花坛,经规划后,南北向要缩短
米的正方形花坛,经规划后,南北向要缩短![]() 米,东西向要加长
米,东西向要加长![]() 米,则改造后花坛的面积是________平方米,改造后花坛的面积减少了________平方米.
米,则改造后花坛的面积是________平方米,改造后花坛的面积减少了________平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y= ![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N. 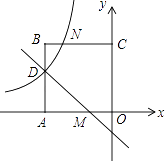
(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )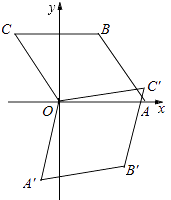
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(2,﹣2)
D.( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com