
【题目】已知:正方形ABCD,E为平面内任意一点,连接DE,将线段DE绕点D顺时针旋转90°得到DG,连接EC,AG.
(1)当点E在正方形ABCD内部时,
①根据题意,在图1中补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG=![]() ,求CE的长.(可在备用图中画图)
,求CE的长.(可在备用图中画图)

【答案】(1) ①见解析;②AG=CE,AG⊥CE,理由见解析;(2)CE的长为![]() 或
或![]()
【解析】
(1)①根据题意补全图形即可;
②先判断出∠GDA=∠EDC,进而得出△AGD≌△CED,即可得出AG=CE,延长CE分别交AG、AD于点F、H,判断出∠AFH=∠HDC=90°即可得出结论;
(2)分两种情况,①当点G在线段BD的延长线上时,②当点G在线段BD上时,构造直角三角形利用勾股定理即可得出结论.
解:(1)当点E在正方形ABCD内部时,
①依题意,补全图形如图1:
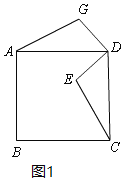
②AG=CE,AG⊥CE.
理由:
在正方形ABCD,
∴AD=CD,∠ADC=90°,
∵由DE绕着点D顺时针旋转90°得DG,
∴∠GDE=∠ADC=90°,GD=DE,
∴∠GDA=∠EDC
在△AGD和△CED中,
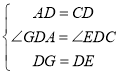 ,
,
∴△AGD≌△CED,
∴AG=CE.
如图2,延长CE分别交AG、AD于点F、H,
∵△AGD≌△CED,
∴∠GAD=∠ECD,
∵∠AHF=∠CHD,
∴∠AFH=∠HDC=90°,
∴AG⊥CE.
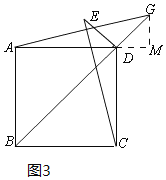
(2)①当点G在线段BD的延长线上时,如图3所示.
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°.
∵GM⊥AD,DG=![]()
∴MD=MG=2,
∴AM=AD+DM=6
在Rt△AMG中,由勾股定理得:AG=![]() =
=![]() ,
,
同(1)可证△AGD≌△CED,
∴CE=AG=![]()
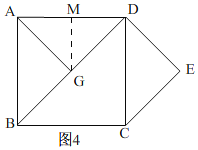
②当点G在线段BD上时,如图4所示,
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADG=45°
∵GM⊥AD,DG=![]()
∴MD=MG=2,
∴AM=AD-MD=2
在Rt△AMG中,由勾股定理得:AG=![]() =
=![]() ,
,
同(1)可证△AGD≌△CED,
∴CE=AG=![]() .
.
故CE的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b,|a﹣15|+(b﹣4.5)2=0,求a,b的值;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=15,AD=2BE,求线段CE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
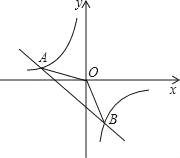
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n).
的图象交于A(﹣2,1),B(1,n).
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△ABO的面积;
(3)根据图象写出使反比例函数的值大于一次函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验证明,平面镜发射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.

(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射,若被b镜反射出的光线n与光线m平行,且∠1=50°,则∠2= ,∠3= ;
(2)在(1)中,若∠1=55°,则∠3= ;若∠1=30°,则∠3= ;
(3)由(1)、(2)请你猜想:当两平面镜a、b的夹角∠3= °时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与发射光线n平行。请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
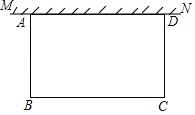
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把六张大小完全相同的小长方形卡片(如图①)不重叠无缝隙的放在一个底面为长方形(长为![]() ,宽为
,宽为![]() )的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长之和是( )
)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长之和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:

(1)阿中总共剪开了几条棱?
(2)现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);
(3)已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某长方形广场长为a米,宽为b米;广场的中间圆形绿地的半径为![]() 米;广场的死角都有一块半径相同的四分之一圆形的绿地,且圆形绿地的半径也为
米;广场的死角都有一块半径相同的四分之一圆形的绿地,且圆形绿地的半径也为![]() 米;
米;

(1)请用代数式分别表示绿地的总面积和空地的面积(结果保留π);
(2)若长方形长为500米,宽为300米,求广场空地的面积。(π取3.14,并保留两个有效数学)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是 ______ ,∠COD的余角是 ______
(2)OE是∠BOC的平分线吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com