
分析 把第一个、第二个、第三个分式的分母因式分解,再把同分母的分式相加即可.
解答 解:原式=$\frac{b-c}{(a-b)(a-c)}$+$\frac{c-a}{(b-c)(b-a)}$+$\frac{a-b}{(c-a)(c-b)}$-$\frac{2}{a-b}$-$\frac{2}{b-c}$-$\frac{2}{c-a}$
=$\frac{1}{a-b}$-$\frac{1}{a-c}$+$\frac{1}{b-c}$-$\frac{1}{b-a}$+$\frac{1}{c-a}$-$\frac{1}{c-b}$-$\frac{2}{a-b}$-$\frac{2}{b-c}$-$\frac{2}{c-a}$
=$\frac{1}{a-b}$+$\frac{1}{c-a}$+$\frac{1}{b-c}$+$\frac{1}{a+b}$+$\frac{1}{c-a}$+$\frac{1}{b-c}$-$\frac{2}{a-b}$-$\frac{2}{b-c}$-$\frac{2}{c-a}$
=0.
点评 本题考查了分式的混合运算,把多项式因式分解是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
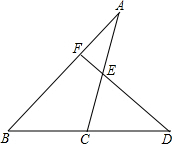 如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数; (2)∠AEF的度数.
如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数; (2)∠AEF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
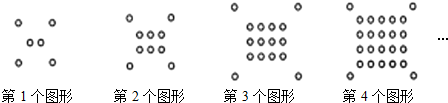
| 图形序号 | 1 | 2 | 3 | 4 | 5 |
| 小圆个数 | 6 | 10 | 16 | 24 | 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com