练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统，图2是某个学生的识别图案，黑色小正方形表示1，白色小正方形表示0.将第一行数字从左到右依次记为，，，，那么可以转换为该生所在班级序号，其序号为.如图2第一行数字从左到右依次为0，1，0，1，序号为，表示该生为5班学生.表示6班学生的识别图案是（ ）

    A. B. C. D.

    【答案】B

    【解析】根据班级序号的计算方法一一进行计算即可.

    【解答】A. 第一行数字从左到右依次为1，0，1，0,序号为，表示该生为10班学生.

    B. 第一行数字从左到右依次为0，1， 1，0，序号为，表示该生为6班学生.

    C. 第一行数字从左到右依次为1，0，0，1，序号为，表示该生为9班学生.

    D. 第一行数字从左到右依次为0，1，1，1，序号为，表示该生为7班学生.

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC中∠B=45°，∠C=30°，点D为BC边上任意一点，连接AD，将线段AD绕A顺时针旋转90°，得到线段AE，连接DE．

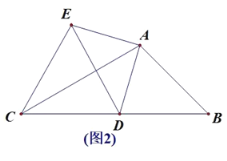
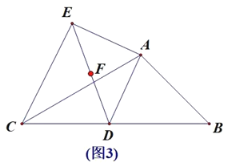
    （1）如图1，点E落在BA的延长线上时，∠EDC= （度）直接填空．

    （2）如图2，点D在运动过程中，DE⊥AC时，AB=4 ，求DE的值．

    （3）如图3，点F为线段DE中点，AB=，求出动点D从B运动到C，点F经过的路径长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，有下列5个结论：①abc＜0；②a－b+c＞0；③ 2a+b=0；④b2-4ac＞0 ⑤a+b+c＞m(am+b)+c，（m＞1的实数），其中正确的结论有（）

    A. 1个 B. 2 C. 3 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，菱形的对角线、相交于点，过点作且，连接、，连接交于点．

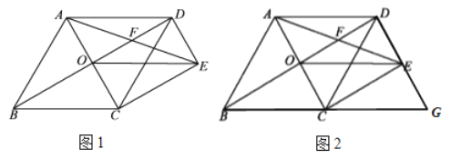
    （1）求证：；

    （2）如图2，延长和相交于点，不添加任何辅助线的情况下，直接写出图中所有的平行四边形．（除四边形和四边形外）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在△ABC中，∠ACB=90°，点D在△ABC外，连接AD，作DE⊥AB，交BC于点F，AD=AB，AE=AC，连接AF，则DF，BC，CF间的等量关系是 ；

    （2）如图2，AB=AD，AC=AE，∠ACB=∠AED=90°，延长BC交DE于点F，写出DF，BC，CF间的等量关系，并证明你的结论.

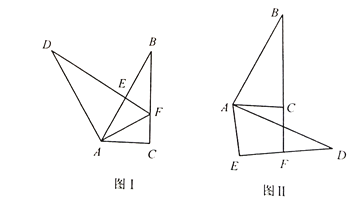
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y1=kx+b的图象与反比例函数的图象交于A（﹣2，1），B（1，n）两点．

    （1）试确定上述反比例函数和一次函数的表达式．

    （2）求△AOB的面积．

    （3）比较y1和y2的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

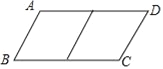
    【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又剩下一个四边形，称为第二次操作；…依此类推，若第n次操作后，余下的四边形是菱形，则称原平行四边形为n阶准菱形，例如：如图1，ABCD中，若AB=1，BC=2，则ABCD为1阶准菱形．

    （1）理解与判断：

    邻边长分别为1和3的平行四边形是　 　阶准菱形；

    邻边长分别为3和4的平行四边形是　 　阶准菱形；

    （2）操作、探究与计算：

    ①已知ABCD的邻边长分别为2，a（a＞2），且是3阶准菱形，请画出ABCD及裁剪线的示意图，并在图形下方写出a的值；

    ②已知ABCD的邻边长分别为a，b（a＞b），满足a=7b+r，b=4r，请写出ABCD是几阶准菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为节约能源，优化电力资源配置，提高电力供应的整体效益，国家实行了错峰用电.某地区的居民用电，按白天时段和晚间时段规定了不同的单价.某户5月份白天时段用电量比晚间时段用电量多，6月份白天时段用电量比5月份白天时段用电量少，结果6月份的总用电量比5月份的总用电量多，但6月份的电费却比5月份的电费少，则该地区晚间时段居民用电的单价比白天时段的单价低的百分数为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ACB＝90°，CD⊥AB，垂足为D，则下面的结论中正确的是（　　）

    ①BC与AC互相垂直；②AC与CD互相垂直；③点A到BC的垂线段是线段BC；④点C到AB的垂线段是线段CD；③线段BC是点B到AC的距离；⑥线段AC的长度是点A到BC的距离．

    A.①④③⑥B.①④⑥C.②③D.①④

    查看答案和解析>>

    同步练习册答案