
【题目】一副三角板按图1所示的位置摆放,将△DEF绕点A.F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为()
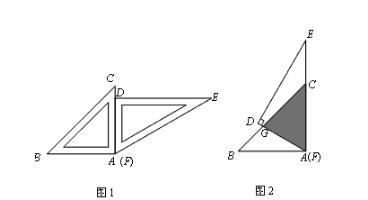
A. 75cm2; B. (25+25![]() )cm2; C. (25+
)cm2; C. (25+![]() )cm2; D. (25+
)cm2; D. (25+![]() )cm2
)cm2
科目:初中数学 来源: 题型:
【题目】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A | B | C | D | E | 平均分 | 方差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| 2 |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
|
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
查看答案和解析>>
科目:初中数学 来源: 题型:
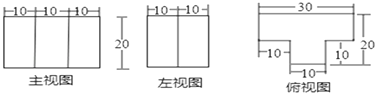
【题目】杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少千克的防锈漆?(铁的密度为7.8g/cm3 ,1千克防锈漆可以涂4m2的铁器面,三视图单位为cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
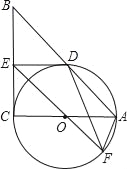
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
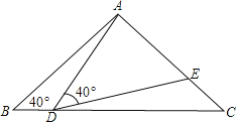
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)点D从B向C运动时,∠BDA逐渐变______(填“大”或“小”);设∠BAD=x°,∠BDA=y°,求y与x的函数关系式;
(2)当DC的长度是多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,当∠BDA等于多少度时,△ADE是等腰三角形?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在_______分钟内,师生不能呆在教室.
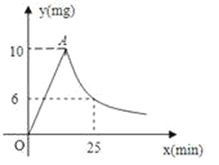
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.
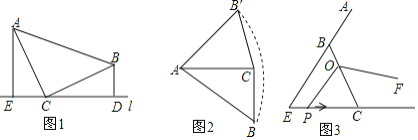
(1)求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=6,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积;
(3)拓展提升:如图3,∠E=60°,EC=EB=4cm,点O在BC上,且OC=3cm,动点P从点E沿射线EC以2cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.在△ABC中,AB=AC,点D为BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F,则四边形AEDF的周长等于这个三角形的( )
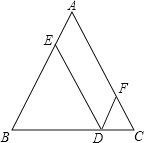
A.周长B.周长的一半
C.两腰长和的一半D.两腰长的和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com